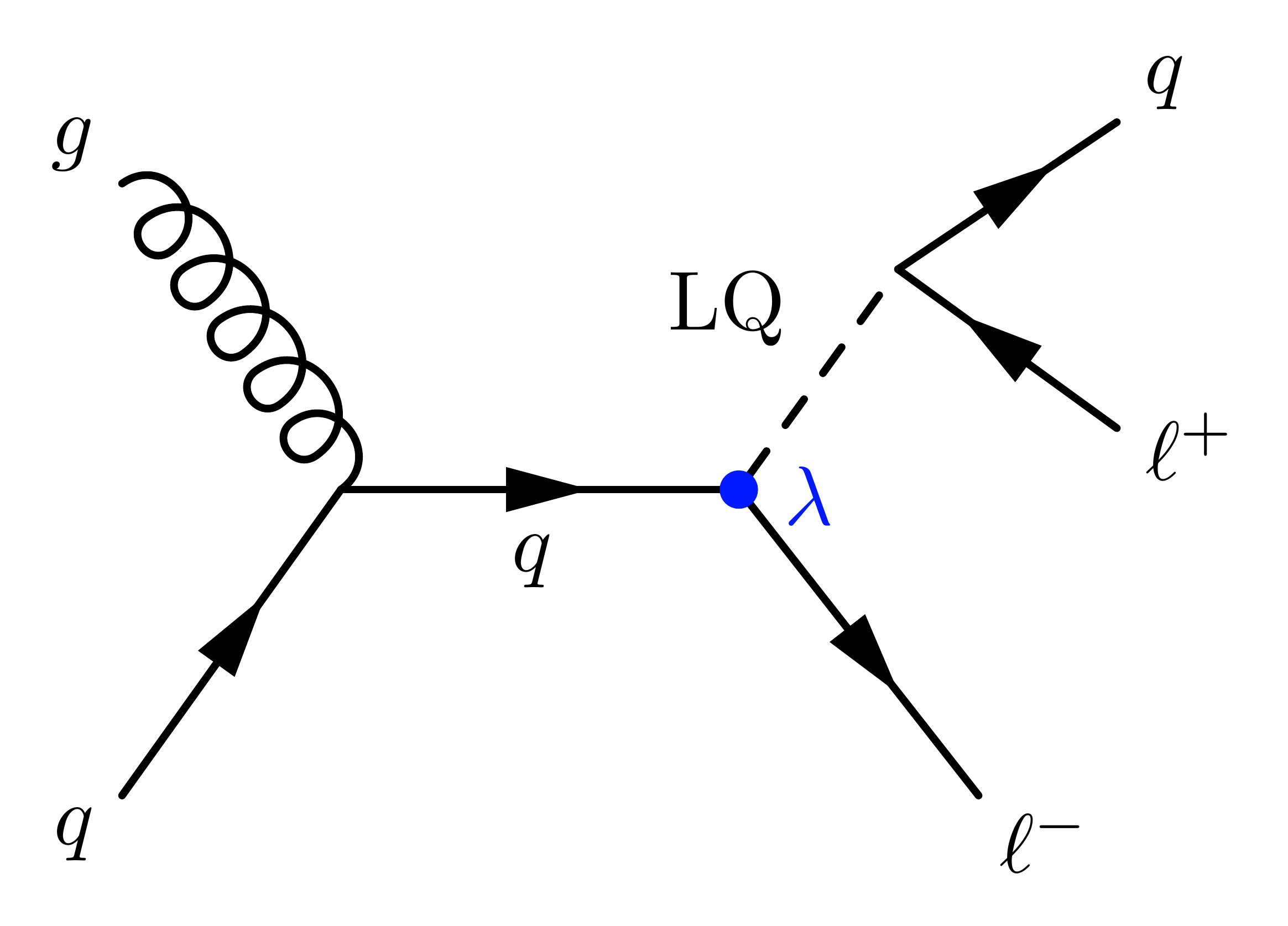
This posts shows code examples of Feynman diagrams of various leptoquark (LQ) production mechanisms in proton-proton collisions at the Large Hadron Collider (LHC). For diagrams of LQ decay, please have a look at this post.
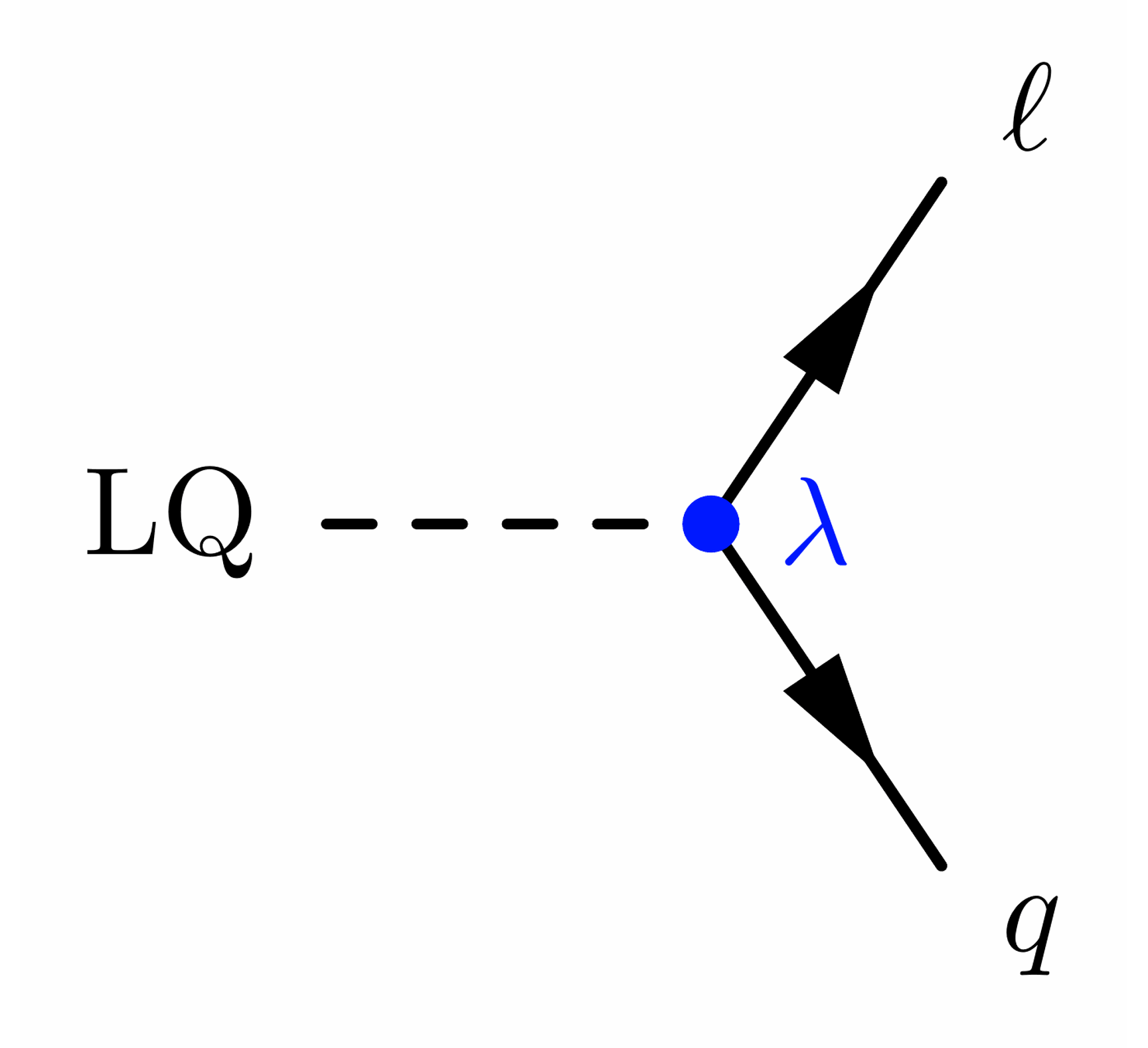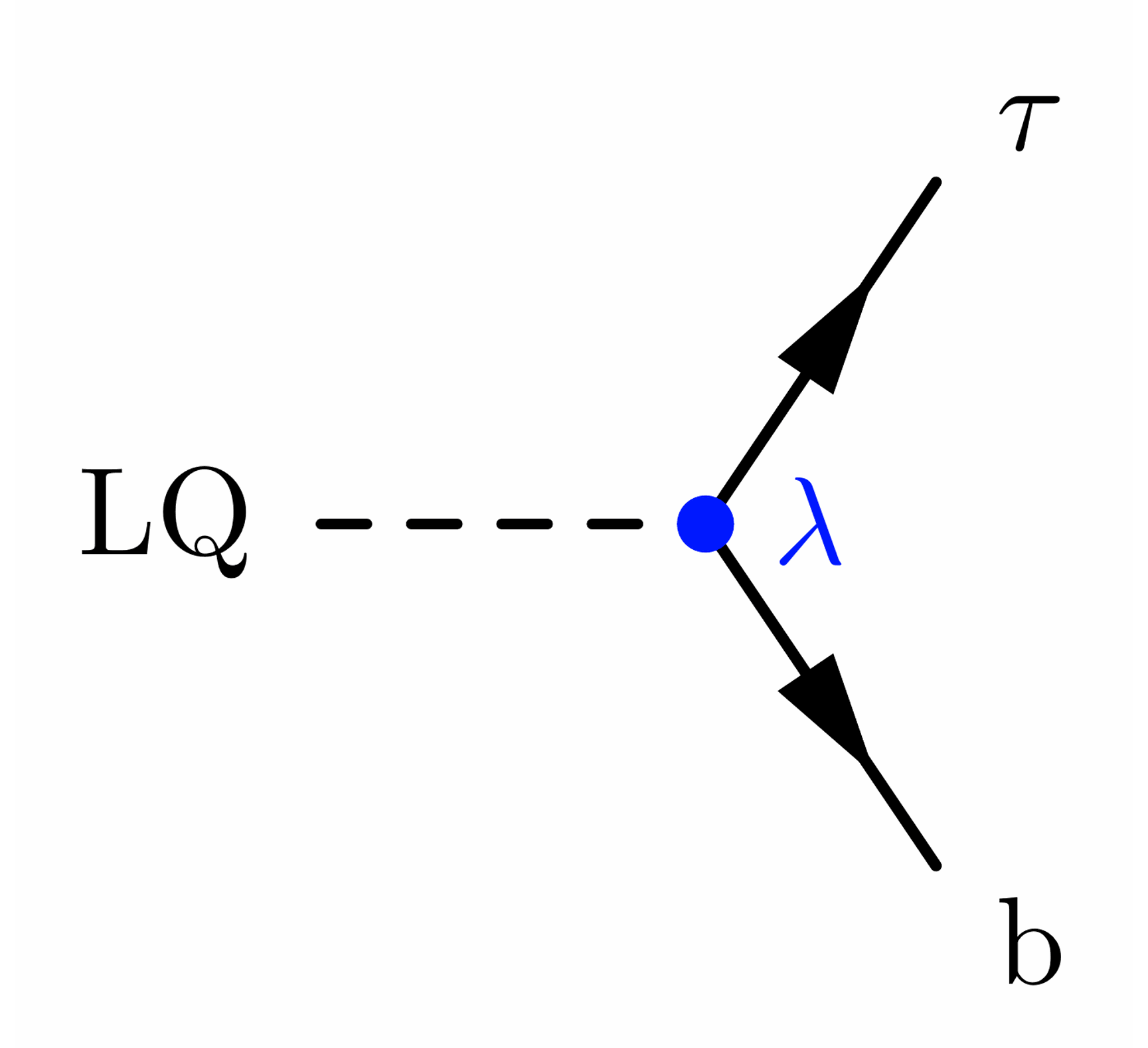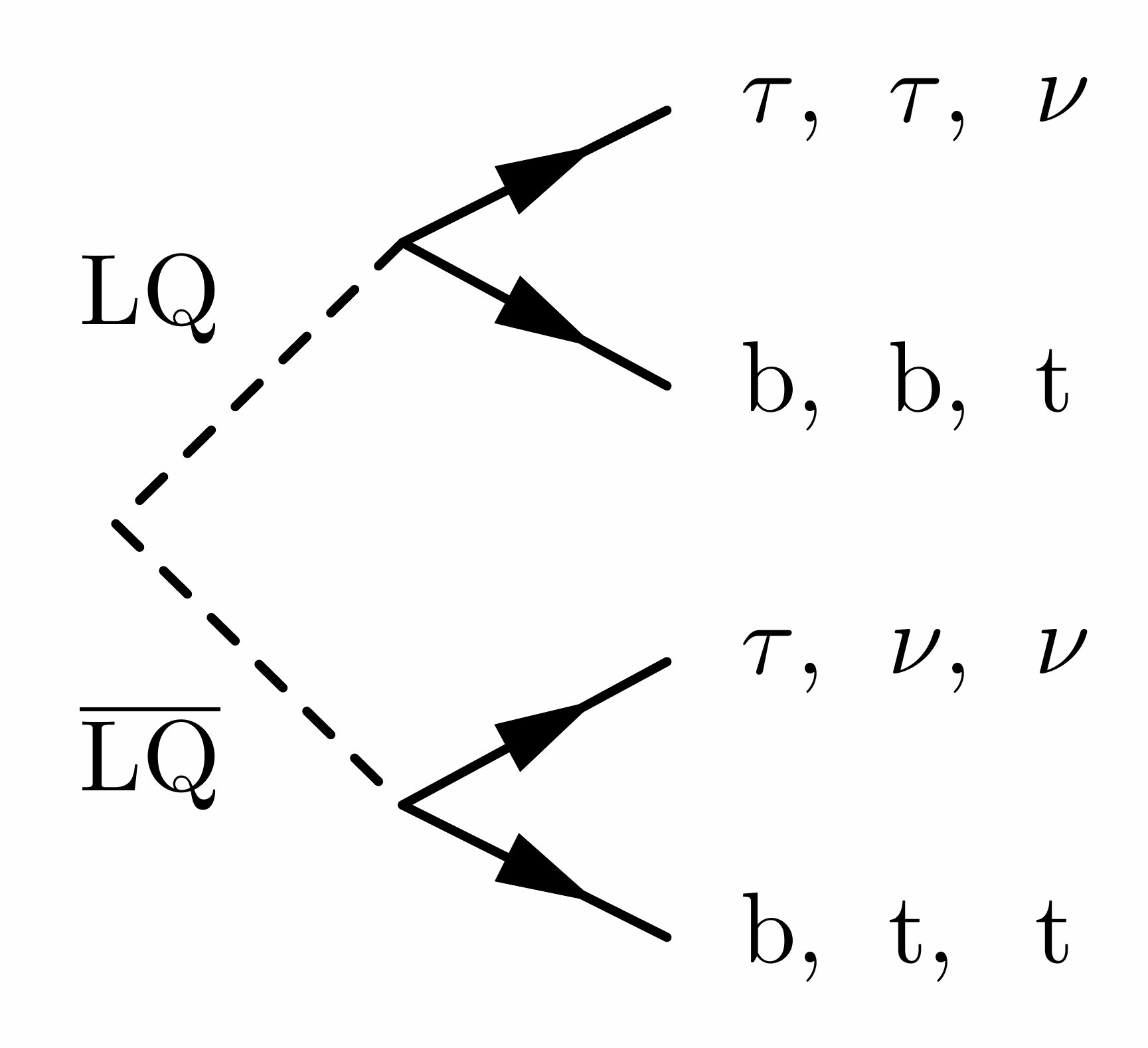
Note that the style convention below uses a dashed line (dashes, dashes_arrow) for the leptoquark, which is similar to that of scalars like the Higgs boson. Some people use double lines (double) instead, or, for vector LQs explicitly, wavy lines (boson) like for the gauge bosons.
Furthermore, the coupling strength between LQs and fermions is indicated with λ in the LQ production vertex to highlight how the cross section tends to scales with λ. Namely, the single production cross section scales with λ2, while the nonresonant production scales with λ4 and pair production does not scale with λ (at leading order). Some references use other symbols like y or g for the coupling strength.
The decays below focus on LQ with dominant couplings to bτ, as this is inspired by my own research (see e.g. this paper by the CMS Collaboration that I worked on as a PhD student).
For more information on LQ models, you can have a look at this great summary by I. Doršner et al., and this graphical representation by myself. For more information on LQ phenomenology at the LHC have a look at the Leptoquark Hunter’s Guide for pair production and large couplings.
Content of this page:
- Single LQ production
- LQ pair production
- Nonresonant dilepton production through t-channel LQ exchange
- Full code
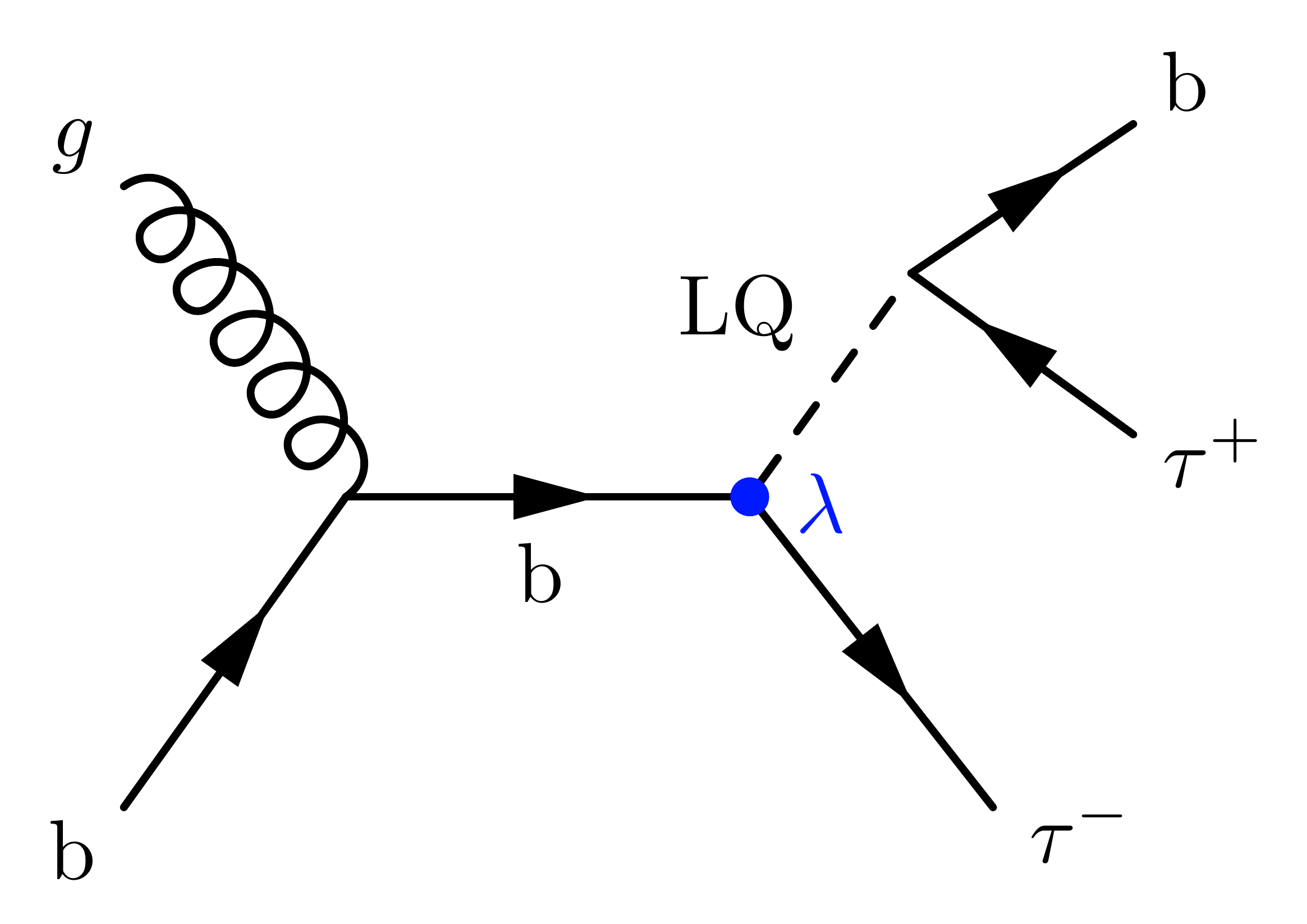
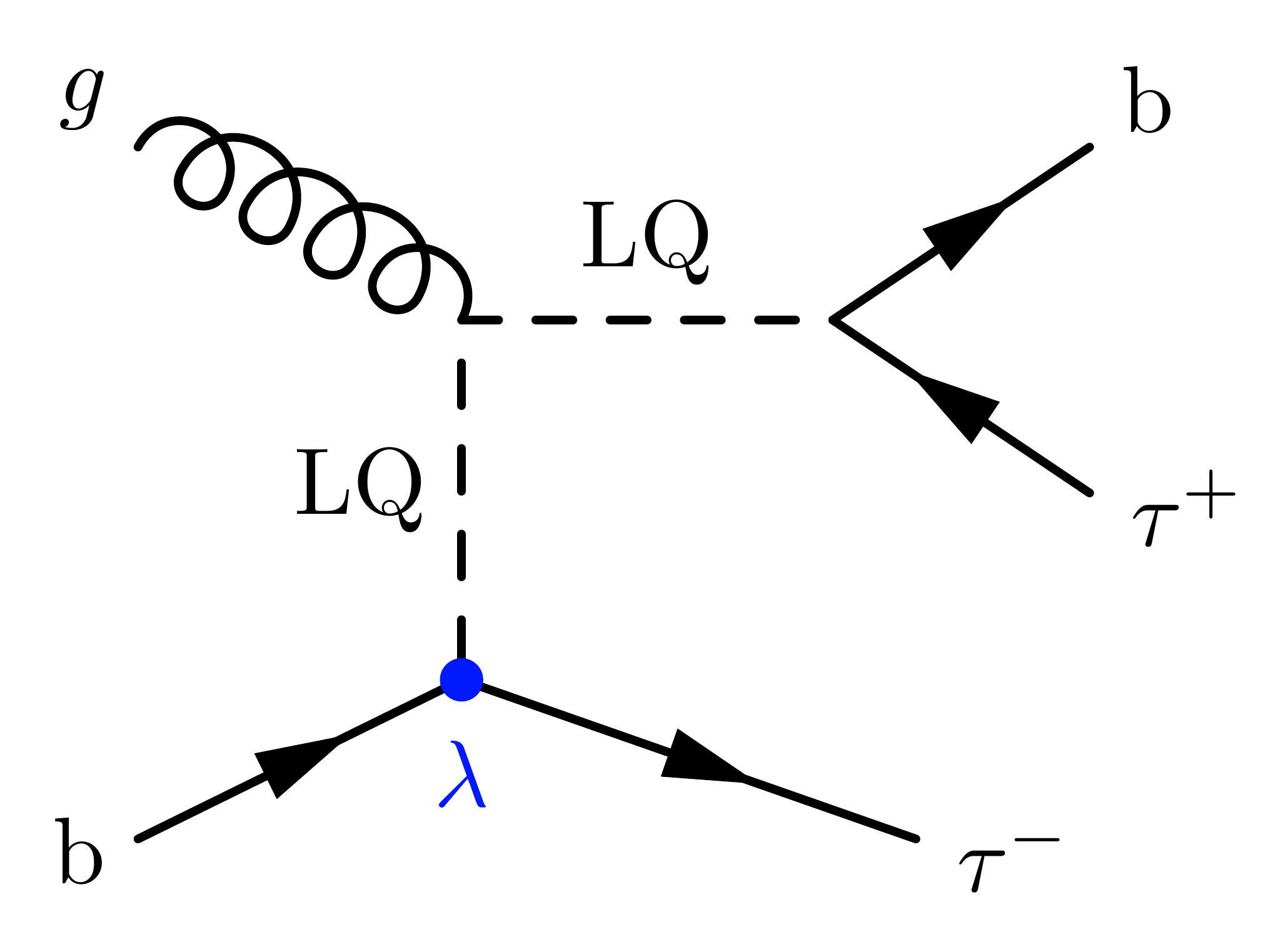
Single LQ production
I call this the “dog diagram”:
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colvtx}{rgb}{0,.1,1} % LQ vertex (blue)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(3,22)(13,15){ % padding (L,T)(R,B)
\begin{fmfgraph*}(130,80) % dimensions (WH)
% line style
\fmfset{dash_len}{10} % dashes length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfstraight
\fmfleft{i2,i1}
\fmfright{o3,o2,o1}
\fmfshift{8 up}{o1,o2}
\fmfshift{18 left}{o3}
% internal vertices (exact placement)
\fmfforce{(.22w,.50h)}{v1} % exact placement
\fmfforce{(.62w,.50h)}{v2} % exact placement
\fmfforce{(.78w,.86h)}{lq} % exact placement
% incoming partons
\fmf{gluon}{v1,i1}
\fmf{fermion}{i2,v1}
% s-channel
\fmf{fermion,l.s=right,label=$q$}{v1,v2}
% associated lepton
\fmf{fermion}{v2,o3}
% LQ -> lepton + quark
\fmf{dashes,t=1.2,l.s=left,label=LQ}{v2,lq}
\fmf{fermion}{o2,lq,o1}
% vertex
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}$\lambda$,l.d=6,l.a=-8}{v2}
% labels
\fmfv{l.a=155,l.d=4,l=$g$}{i1}
\fmfv{l.a=-155,l.d=4,l=$q$}{i2}
\fmfv{l.a=25,l.d=4,l=$q$}{o1}
\fmfv{l.a=-20,l.d=4,l=\vspace{-2pt}$\ell^+$}{o2}
\fmfv{l.a=-25,l.d=3,l=$\ell^-$}{o3}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colvtx}{rgb}{0,.1,1} % LQ vertex (blue)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(3,22)(13,13){ % padding (L,T)(R,B)
\begin{fmfgraph*}(130,80) % dimensions (WH)
% line style
\fmfset{dash_len}{10} % dashes length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfstraight
\fmfleft{i2,i1}
\fmfright{o3,o2,o1}
\fmfshift{8 up}{o1,o2}
\fmfshift{18 left}{o3}
% internal vertices (exact placement)
\fmfforce{(.22w,.50h)}{v1} % exact placement
\fmfforce{(.62w,.50h)}{v2} % exact placement
\fmfforce{(.78w,.86h)}{lq} % exact placement
% incoming partons
\fmf{gluon}{v1,i1}
\fmf{fermion}{i2,v1}
% s-channel
\fmf{fermion,l.s=right,label=b}{v1,v2}
% associated lepton
\fmf{fermion}{v2,o3}
% LQ -> lepton + quark
\fmf{dashes,t=1.2,l.s=left,label=LQ}{v2,lq}
\fmf{fermion}{o2,lq,o1}
% vertex
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}$\lambda$,l.d=6,l.a=-8}{v2}
% labels
\fmfv{l.a=155,l.d=4,l=$g$}{i1}
\fmfv{l.a=-155,l.d=4,l=b}{i2}
\fmfv{l.a=25,l.d=4,l=b}{o1}
\fmfv{l.a=-20,l.d=4,l=\vspace{-2pt}$\tau^+$}{o2}
\fmfv{l.a=-20,l.d=5,l=\vspace{-2pt}$\tau^-$}{o3}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
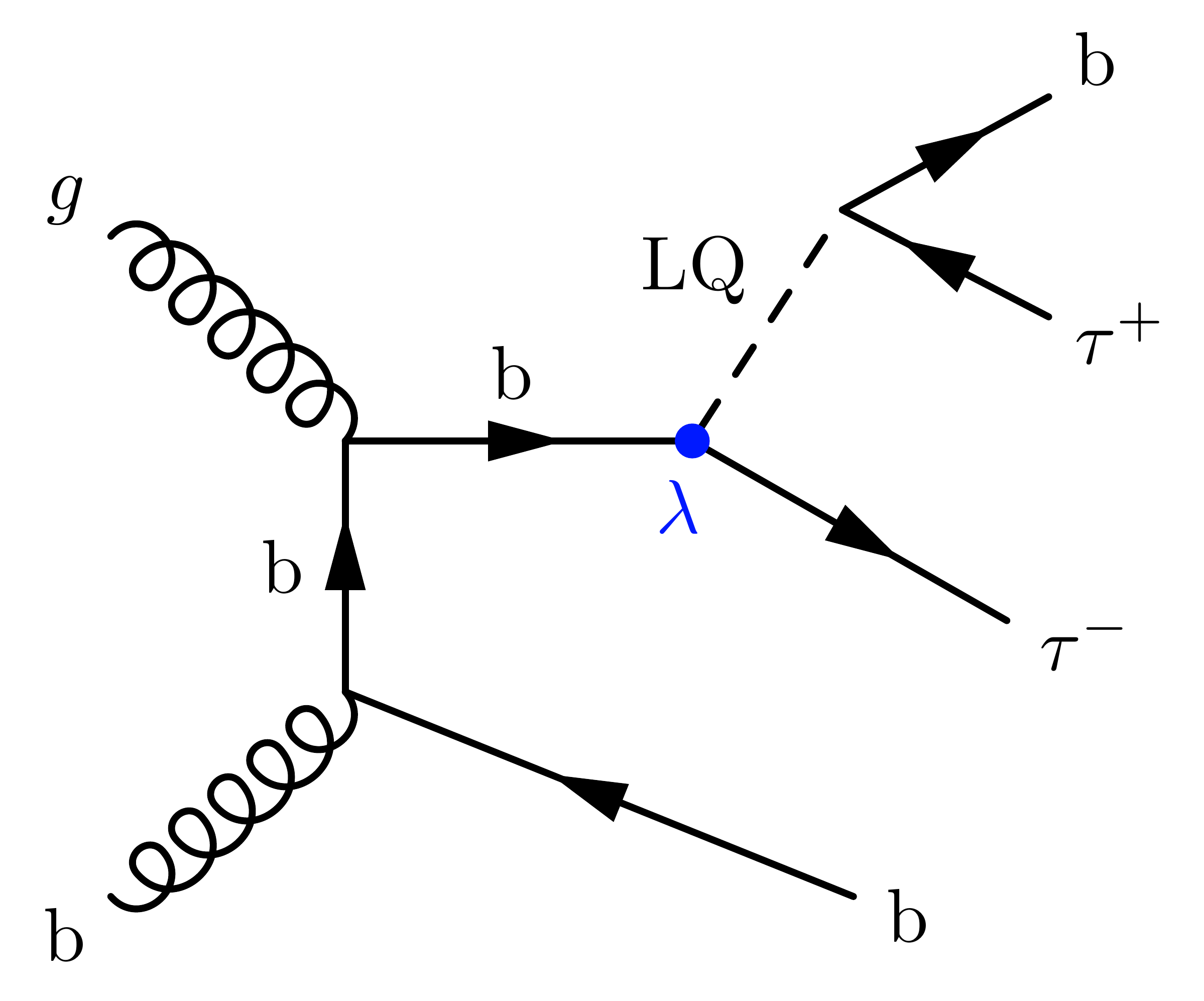
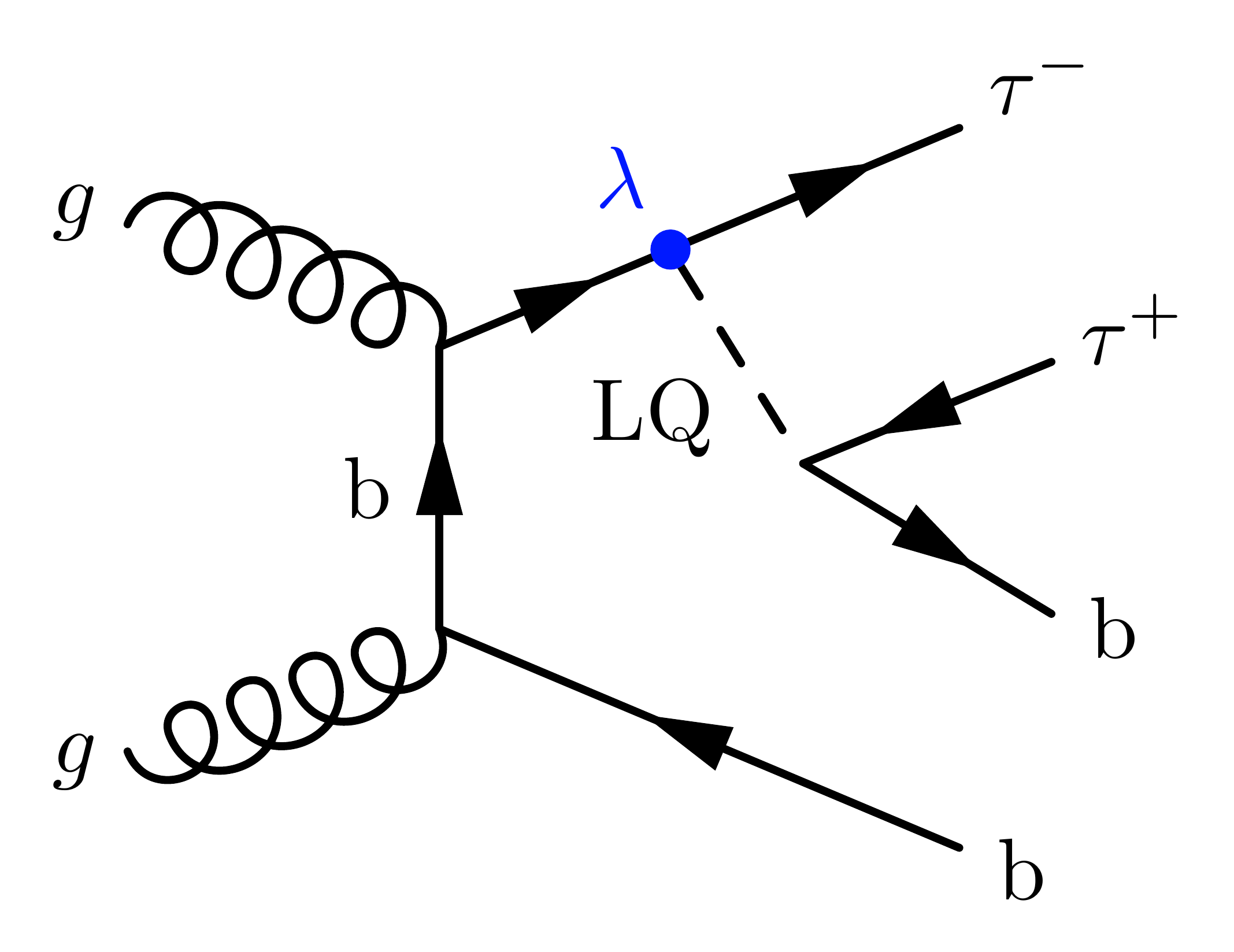
With an incoming bottom quark from gluon splitting, adding a second bottom quark to the final state:
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colvtx}{rgb}{0,.1,1} % LQ vertex (blue)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(3,32)(13,13){ % padding (L,T)(R,B)
\begin{fmfgraph*}(135,95) % dimensions (WH)
% line style
\fmfset{dash_len}{10} % dashes length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfstraight
\fmfleft{i2,i1}
\fmfright{o4,o3,o2,o1}
\fmfshift{20 up}{o1,o2}
\fmfshift{8 up}{o3}
\fmfshift{6 left}{o3}
\fmfshift{28 left}{o4}
% internal vertices (exact placement)
\fmfforce{(.25w,.31h)}{vg} % exact placement
\fmfforce{(.25w,.69h)}{v1} % exact placement
\fmfforce{(.62w,.69h)}{v2} % exact placement
\fmfforce{(.78w,1.04h)}{lq} % exact placement
% gluon splitting
\fmf{gluon}{v1,i1}
\fmf{gluon}{i2,vg}
\fmf{fermion,l.s=left,label=b}{vg,v1}
\fmf{fermion}{o4,vg}
% s-channel
\fmf{fermion,l.s=left,label=b}{v1,v2}
% associated lepton
\fmf{fermion}{v2,o3}
% LQ -> lepton + quark
\fmf{dashes,t=1.2,l.d=4,l.s=left,label=LQ}{v2,lq}
\fmf{fermion}{o2,lq,o1}
% vertex
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}$\lambda$,l.d=6,l.a=-110}{v2}
% labels
\fmfv{l.a=155,l.d=4,l=$g$}{i1}
\fmfv{l.a=-155,l.d=4,l=b}{i2}
\fmfv{l.a=25,l.d=4,l=b}{o1}
\fmfv{l.a=-20,l.d=4,l=\vspace{-2pt}$\tau^+$}{o2}
\fmfv{l.a=-20,l.d=5,l=\vspace{-2pt}$\tau^-$}{o3}
\fmfv{l.a=-20,l.d=5,l=\vspace{-2pt}b}{o4}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colvtx}{rgb}{0,.1,1} % LQ vertex (blue)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(-10,14)(12,11){ % padding (L,T)(R,B)
\begin{fmfgraph*}(130,90) % dimensions (WH)
% line style
\fmfset{dash_len}{10} % dashes length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfleft{i2,i1}
\fmfright{o4,o3,o2,o1}
\fmfshift{12 down}{i1}
\fmfshift{12 up}{i2}
% gluon splitting
\fmf{gluon}{v1,i1}
\fmf{gluon}{i2,v2}
\fmf{fermion,t=0.9,l.s=left,label=b}{v2,v1} % t-channel
\fmf{phantom,t=0.6}{v1,o1,o4,v2}
\fmffreeze
% outgoing bottom quarks
\fmf{fermion}{v1,lq1}
\fmf{fermion,t=0.8}{lq1,o1}
\fmf{fermion}{o4,v2}
\fmffreeze
% LQ -> btau
\fmf{dashes,t=0.9,l.s=right,l.d=4,label=LQ}{lq1,lq2}
\fmf{fermion,t=0.9}{o2,lq2,o3}
\fmf{phantom,t=0.9}{v2,lq2}
% vertex
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}$\lambda$,l.d=6,l.a=120}{lq1}
% labels
\fmfv{l.a=160,l.d=4,l=$g$}{i1}
\fmfv{l.a=-160,l.d=4,l=$g$}{i2}
\fmfv{l.a=25,l.d=4,l=$\tau^-$}{o1}
\fmfv{l.a=25,l.d=4,l=\vspace{-2pt}$\tau^+$}{o2}
\fmfv{l.a=-20,l.d=5,l=b}{o3}
\fmfv{l.a=-20,l.d=5,l=\vspace{-2pt}b}{o4}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colvtx}{rgb}{0,.1,1} % LQ vertex (blue)
\definecolor{colqcd}{rgb}{1,0,0} % strong vertex (red)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(3,15)(13,11){ % padding (L,T)(R,B)
\begin{fmfgraph*}(110,80) % dimensions (WH)
% line style
\fmfset{dash_len}{10} % dashes length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfstraight
\fmfleft{i2,i1}
\fmfright{o3,o2,o1}
\fmfshift{20 left}{o3}
% internal vertices (exact placement)
\fmfforce{(.34w,.75h)}{v1} % exact placement
\fmfforce{(.34w,.23h)}{v2} % exact placement
\fmfforce{(.73w,.75h)}{lq} % exact placement
\fmffreeze
% gluon + quarks
\fmf{gluon}{v1,i1}
\fmf{fermion}{i2,v2,o3}
% LQs
\fmf{dashes,t=1.2,l.s=left,l.d=4,label=LQ}{v1,lq}
\fmf{dashes,l.s=left,l.d=4,label=LQ}{v2,v1}
% LQ -> lepton + quark
\fmf{fermion}{o2,lq,o1}
% vertex
%\fmfv{d.sh=circle,d.f=full,d.si=4,f=(1,,0,,0),
% l=\color{colqcd}$\alpha_\mathrm{s}$,l.d=5,l.a=-40}{v1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}$\lambda$,l.d=7,l.a=-90}{v2}
% labels
\fmfv{l.a=150,l.d=4,l=$g$}{i1}
\fmfv{l.a=-160,l.d=4,l=b}{i2}
\fmfv{l.a=-20,l.d=5,l=$\tau^-$}{o3}
\fmfv{l.a=25,l.d=4,l=b}{o1}
\fmfv{l.a=-20,l.d=5,l=$\tau^+$}{o2}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
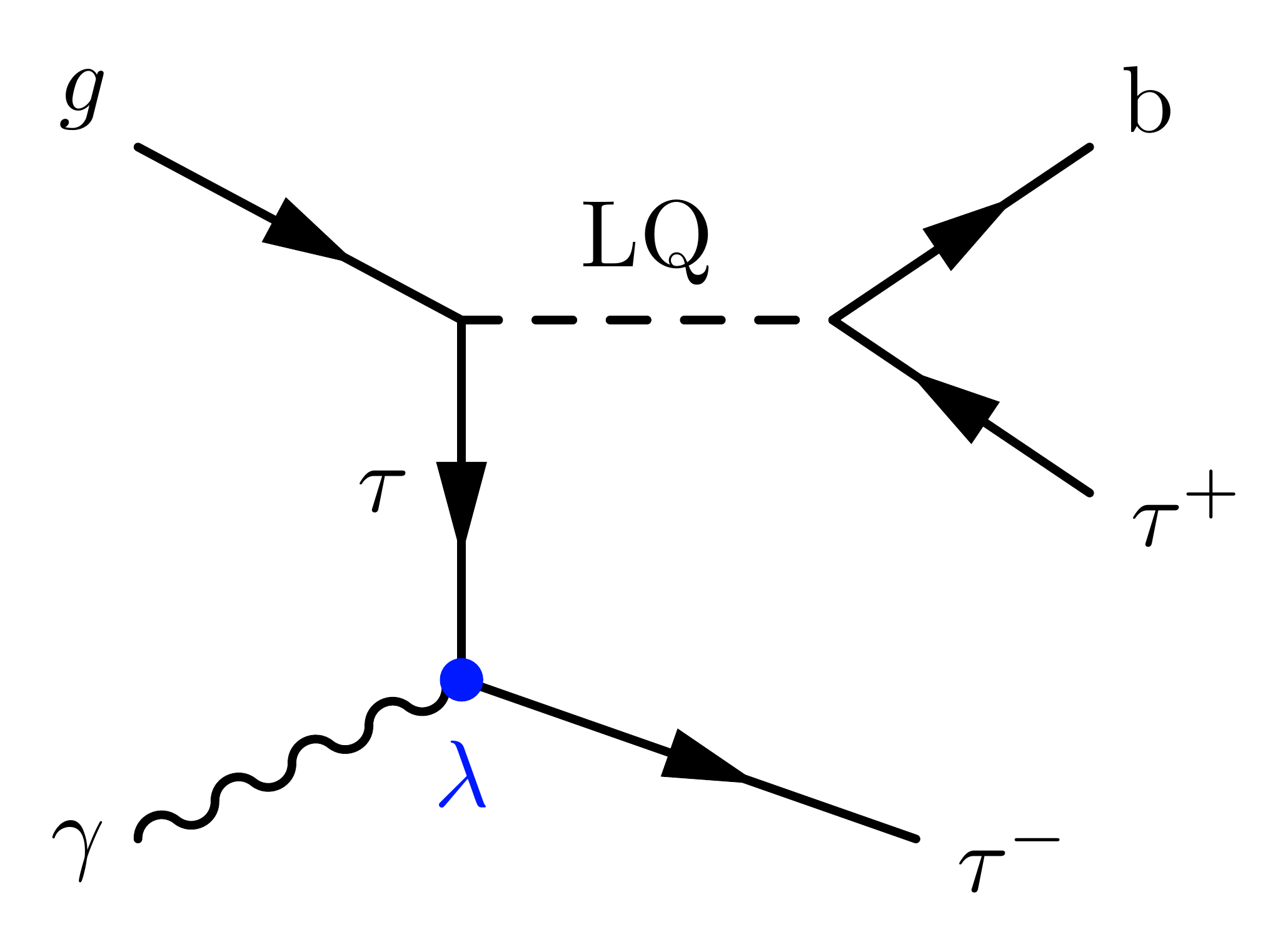
Photon-induced single LQ production:
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colvtx}{rgb}{0,.1,1} % LQ vertex (blue)
\definecolor{colqcd}{rgb}{1,0,0} % strong vertex (red)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(3,15)(13,11){ % padding (L,T)(R,B)
\begin{fmfgraph*}(110,80) % dimensions (WH)
% line style
\fmfset{dash_len}{10} % dashes length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfstraight
\fmfleft{i2,i1}
\fmfright{o3,o2,o1}
\fmfshift{20 left}{o3}
% internal vertices (exact placement)
\fmfforce{(.34w,.75h)}{v1} % exact placement
\fmfforce{(.34w,.23h)}{v2} % exact placement
\fmfforce{(.73w,.75h)}{lq} % exact placement
\fmffreeze
% gluon + quarks
\fmf{fermion}{i1,v1}
\fmf{photon}{i2,v2} % photon
\fmf{fermion}{v2,o3}
% LQs
\fmf{dashes,t=1.2,l.s=left,l.d=4,label=LQ}{v1,lq}
\fmf{fermion,l.s=right,label=$\tau$}{v1,v2}
% LQ -> lepton + quark
\fmf{fermion}{o2,lq,o1}
% vertex
%\fmfv{d.sh=circle,d.f=full,d.si=4,f=(1,,0,,0),
% l=\color{colqcd}$\alpha_\mathrm{s}$,l.d=5,l.a=-40}{v1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}$\lambda$,l.d=7,l.a=-90}{v2}
% labels
\fmfv{l.a=150,l.d=4,l=$g$}{i1}
\fmfv{l.a=-160,l.d=4,l=$\gamma$}{i2}
\fmfv{l.a=-20,l.d=5,l=$\tau^-$}{o3}
\fmfv{l.a=25,l.d=4,l=b}{o1}
\fmfv{l.a=-20,l.d=5,l=$\tau^+$}{o2}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
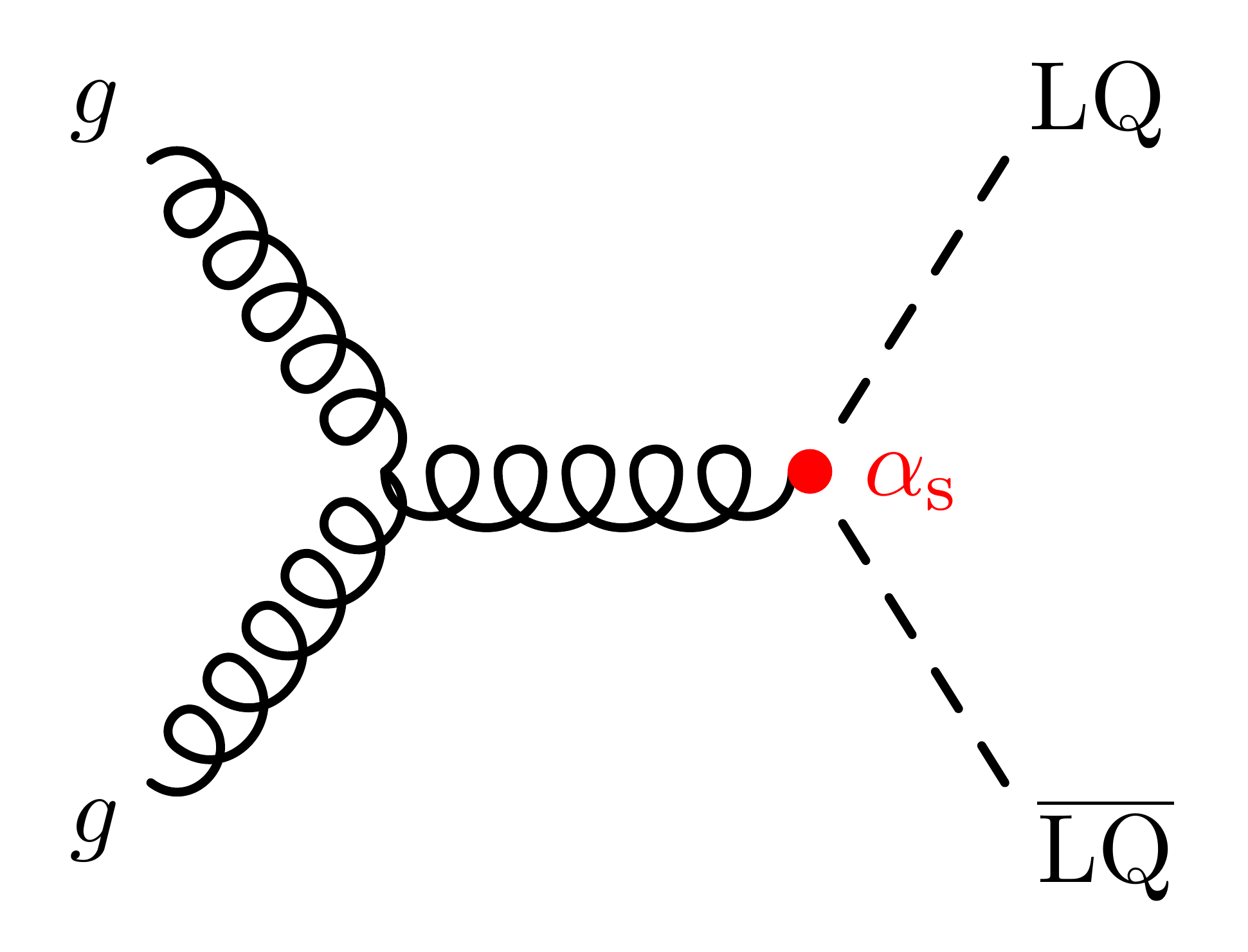
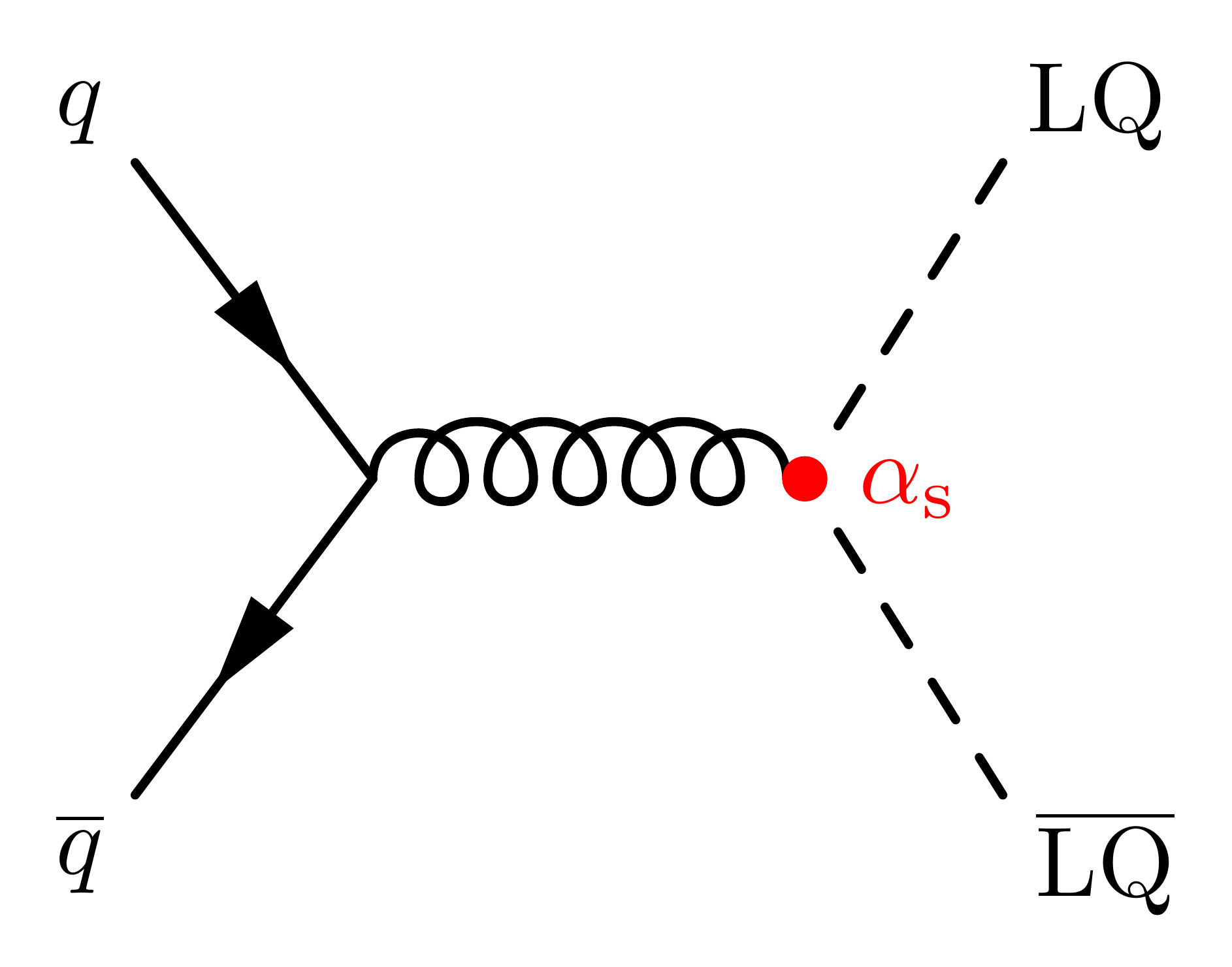
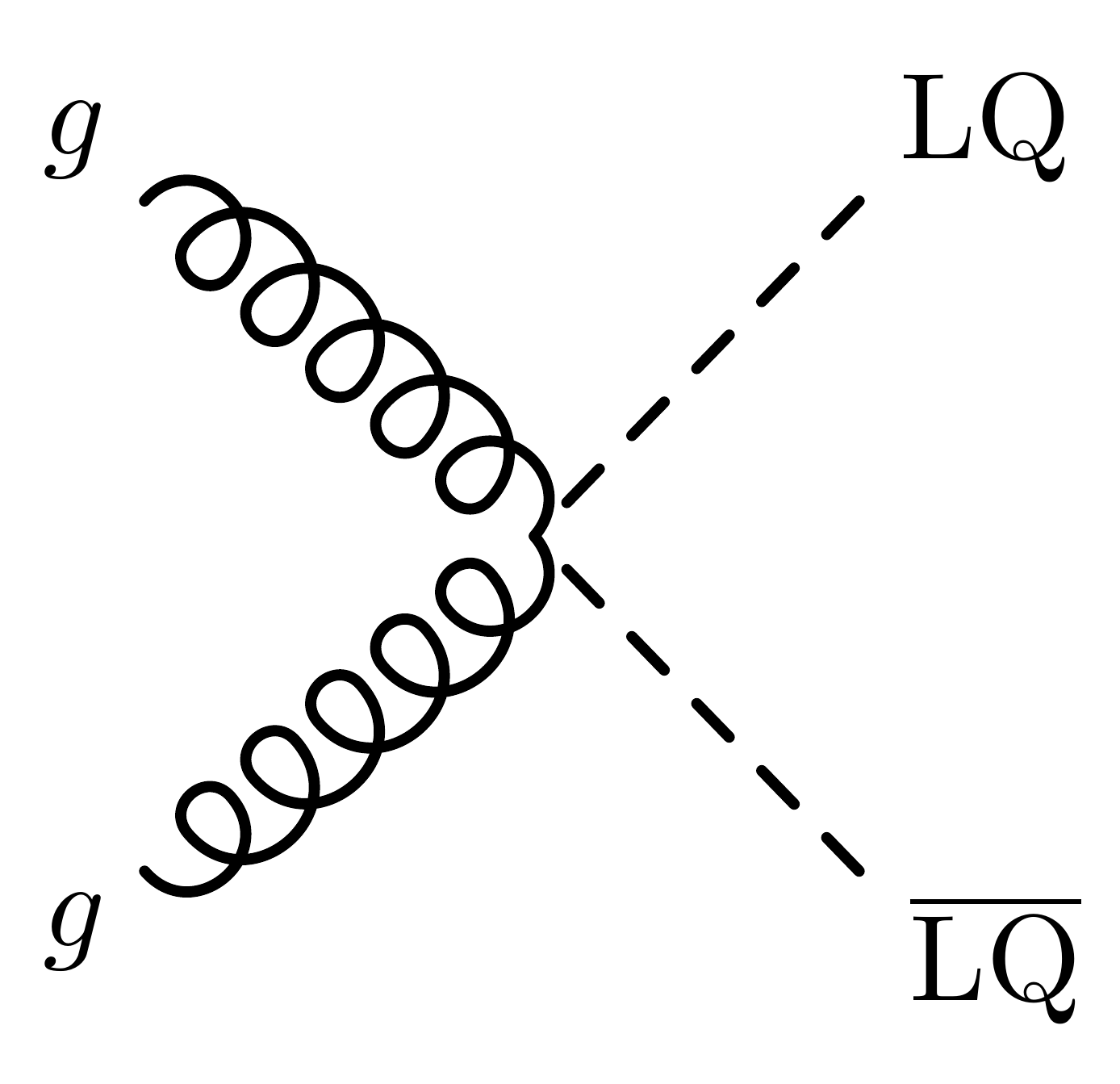
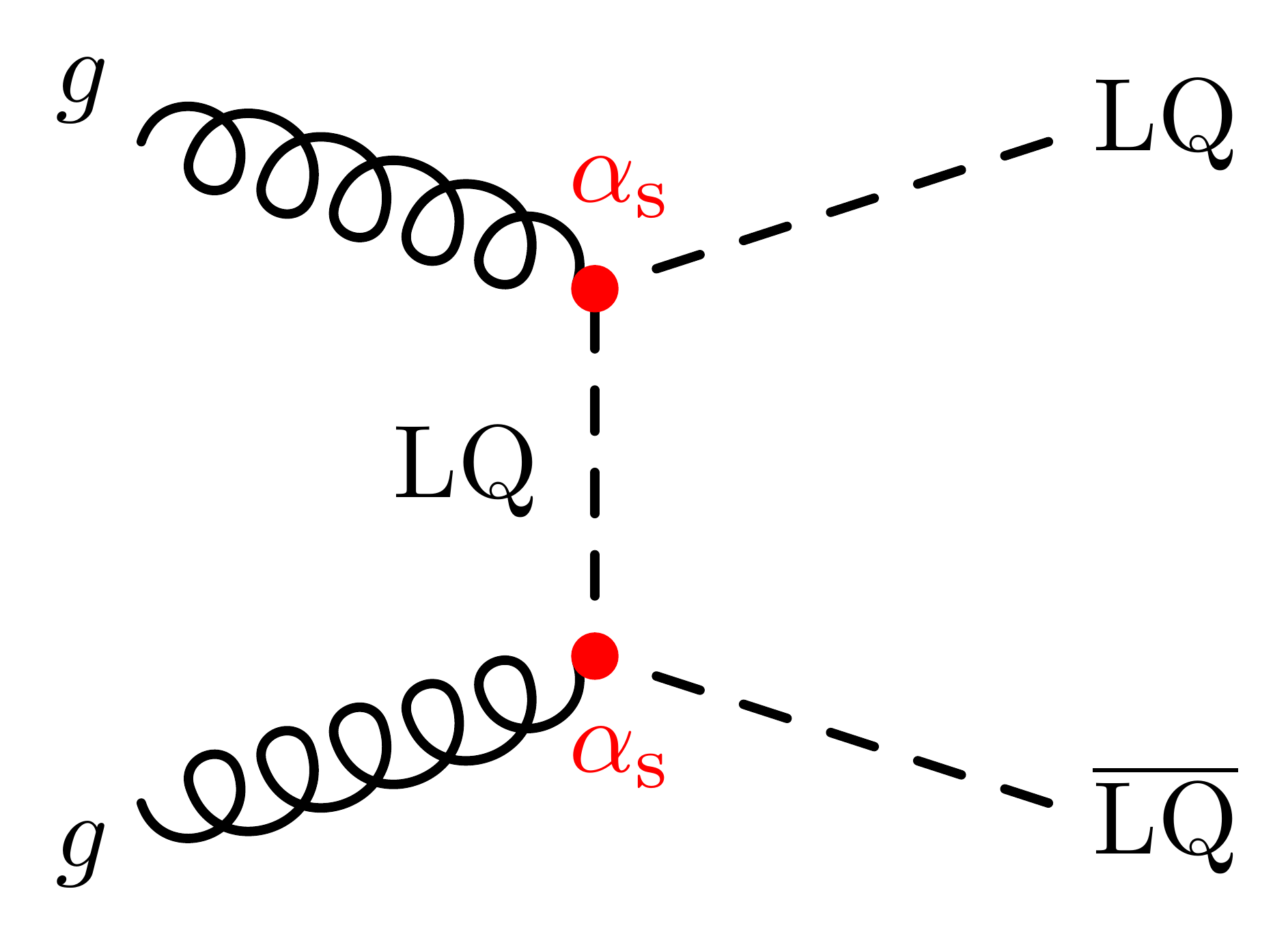
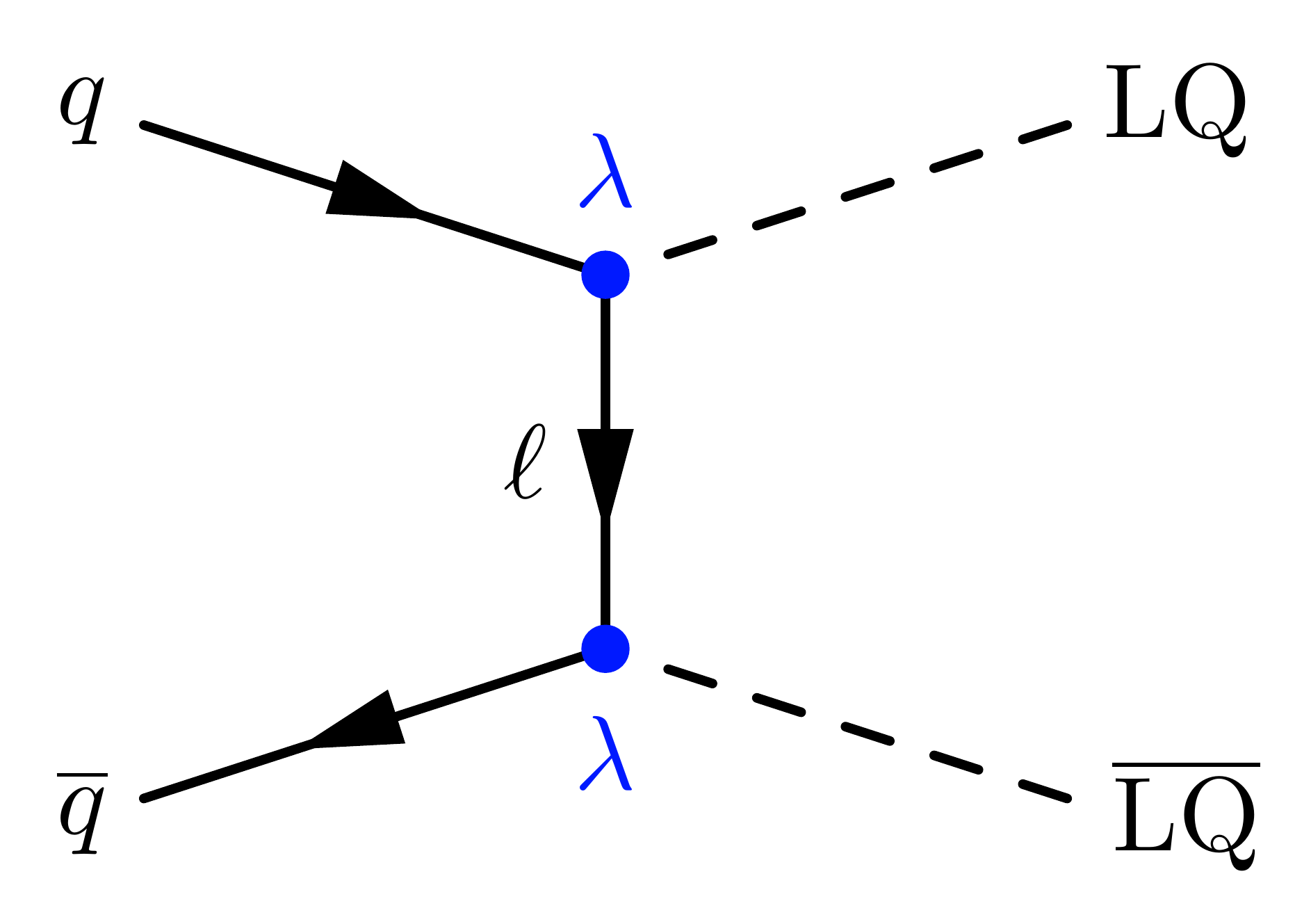
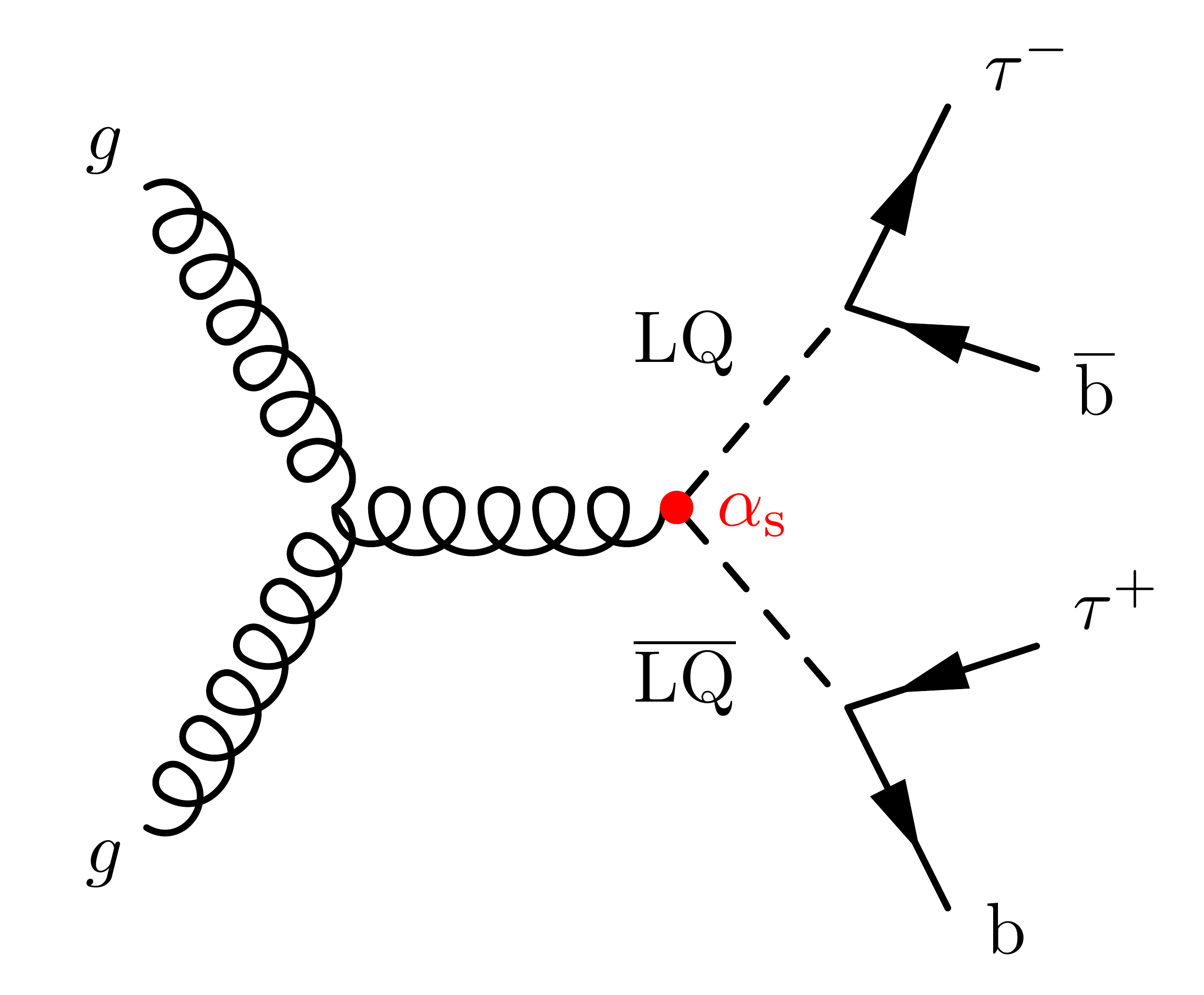
LQ pair production
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colqcd}{rgb}{1,0,0} % strong vertex (red)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(-8,16)(6,17){ % padding (L,T)(R,B)
\begin{fmfgraph*}(120,70) % dimensions (WH)
% line style
\fmfset{dash_len}{10} % dashes length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfleft{i2,i1}
\fmfright{o2,o1}
% gg -> g
\fmf{gluon}{i2,v1,i1}
\fmf{gluon,t=1.1}{v1,v2} % s-channel
% g -> LQ LQ
\fmf{dashes,t=1.2}{o1,v2}
\fmf{dashes,t=1.2}{o2,v2}
% vertex
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(1,,0,,0),
l=\strut\color{colqcd}$\alpha_\mathrm{s}$,l.d=6,l.a=0}{v2}
% labels
\fmfv{l.a=150,l.d=4,l=$g$}{i1}
\fmfv{l.a=-150,l.d=4,l=$g$}{i2}
\fmfv{l.a=25,l.d=3,l=LQ}{o1}
\fmfv{l.a=-25,l.d=4,l=$\overline{\mathrm{LQ}}$}{o2}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colqcd}{rgb}{1,0,0} % strong vertex (red)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(-10,16)(4,17){ % padding (L,T)(R,B)
\begin{fmfgraph*}(120,70) % dimensions (WH)
% line style
\fmfset{dash_len}{10} % dashes length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfleft{i2,i1}
\fmfright{o2,o1}
% gg -> g
\fmf{fermion}{i1,v1,i2}
\fmf{gluon,t=1.1}{v2,v1} % s-channel
% g -> LQ LQ
\fmf{dashes,t=1.2}{o1,v2}
\fmf{dashes,t=1.2}{o2,v2}
% vertex
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(1,,0,,0),
l=\strut\color{colqcd}$\alpha_\mathrm{s}$,l.d=6,l.a=0}{v2}
% labels
\fmfv{l.a=150,l.d=4,l=$q$}{i1}
\fmfv{l.a=-150,l.d=4,l=$\overline{q}$}{i2}
\fmfv{l.a=25,l.d=3,l=LQ}{o1}
\fmfv{l.a=-25,l.d=4,l=$\overline{\mathrm{LQ}}$}{o2}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colqcd}{rgb}{1,0,0} % strong vertex (red)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(-8,16)(6,17){ % padding (L,T)(R,B)
\begin{fmfgraph*}(80,60) % dimensions (WH)
% line style
\fmfset{dash_len}{10} % dashes length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfleft{i2,i1}
\fmfright{o2,o1}
% gg -> g
\fmf{gluon}{i2,v,i1}
% g -> LQ LQ
\fmf{dashes,t=1.2}{o1,v}
\fmf{dashes,t=1.2}{o2,v}
% vertex
%\fmfv{d.sh=circle,d.f=full,d.si=4,f=(1,,0,,0),
% l=\strut\color{colqcd}$\alpha_\mathrm{s}$,l.d=6,l.a=0}{v}
% labels
\fmfv{l.a=150,l.d=4,l=$g$}{i1}
\fmfv{l.a=-150,l.d=4,l=$g$}{i2}
\fmfv{l.a=25,l.d=4,l=LQ}{o1}
\fmfv{l.a=-25,l.d=5,l=$\overline{\mathrm{LQ}}$}{o2}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colqcd}{rgb}{1,0,0} % strong vertex (red)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(-10,13)(4,13){ % padding (L,T)(R,B)
\begin{fmfgraph*}(120,70) % dimensions (WH)
% line style
\fmfset{dash_len}{10} % dashes length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfleft{i2,i1}
\fmfright{o2,o1}
% gg -> LQ LQ
\fmf{gluon}{v1,i1}
\fmf{gluon}{i2,v2}
\fmf{dashes,t=0.8,l.s=right,label=LQ}{v1,v2} % t-channel
% outgoing LQs
\fmf{dashes}{o1,v1}
\fmf{dashes}{o2,v2}
% vertices
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(1,,0,,0),
l=\color{colqcd}$\alpha_\mathrm{s}$,l.d=8,l.a=70}{v1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(1,,0,,0),
l=\color{colqcd}$\alpha_\mathrm{s}$,l.d=8,l.a=-70}{v2}
% labels
\fmfv{l.a=150,l.d=4,l=$g$}{i1}
\fmfv{l.a=-150,l.d=4,l=$g$}{i2}
\fmfv{l.a=20,l.d=5,l=LQ}{o1}
\fmfv{l.a=-20,l.d=5,l=$\overline{\mathrm{LQ}}$}{o2}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colvtx}{rgb}{0,.1,1} % LQ vertex (blue)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(-10,11)(4,11){ % padding (L,T)(R,B)
\begin{fmfgraph*}(120,70) % dimensions (WH)
% line style
\fmfset{dash_len}{10} % dashes length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfleft{i2,i1}
\fmfright{o2,o1}
% qq -> LQ LQ
\fmf{fermion}{i1,v1}
\fmf{fermion}{v2,i2}
\fmf{fermion,t=0.8,l.s=right,label=$\ell$}{v1,v2} % t-channel
% outgoing LQs
\fmf{dashes}{o1,v1}
\fmf{dashes}{o2,v2}
% vertices
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}$\lambda$,l.d=7,l.a=90}{v1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}$\lambda$,l.d=7,l.a=-90}{v2}
% labels
\fmfv{l.a=160,l.d=4,l=$q$}{i1}
\fmfv{l.a=-160,l.d=4,l=$\overline{q}$}{i2}
\fmfv{l.a=20,l.d=4,l=LQ}{o1}
\fmfv{l.a=-20,l.d=5,l=$\overline{\mathrm{LQ}}$}{o2}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colqcd}{rgb}{1,0,0} % strong vertex (red)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(3,14)(14,11){ % padding (L,T)(R,B)
\begin{fmfgraph*}(140,100) % dimensions (WH)
% line style
\fmfset{dash_len}{10} % dashes length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfstraight
\fmfleft{i2,i1}
\fmfright{o4,o3,o2,o1}
\fmfshift{10 down}{i1}
\fmfshift{10 up}{i2}
% internal vertices (exact placement)
\fmfforce{(.80w,.82h)}{lq1} % exact placement
\fmfforce{(.80w,.18h)}{lq2} % exact placement
% gg -> g
\fmf{gluon}{v1,i1}
\fmf{gluon}{i2,v1}
\fmf{gluon,t=1.1}{v1,v2} % s-channel
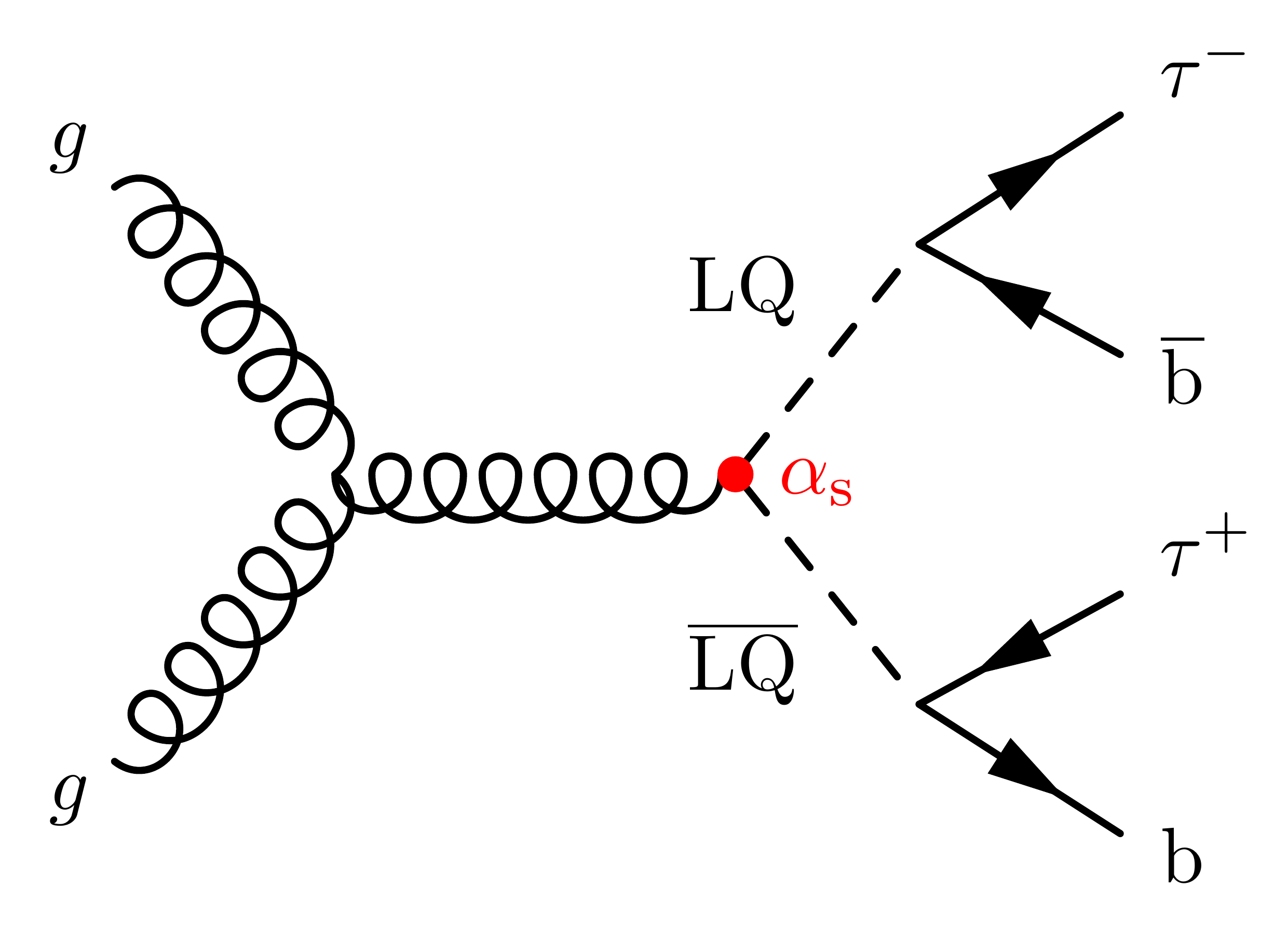
% g -> LQ LQ
\fmf{dashes,t=1.2,l.s=left,label=LQ}{v2,lq1}
\fmf{dashes,t=1.2,l.s=right,label=$\overline{\mathrm{LQ}}$}{v2,lq2}
% LQ -> ql
\fmf{fermion}{o2,lq1,o1}
\fmf{fermion}{o3,lq2,o4}
% vertex
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(1,,0,,0),
l=\strut\color{colqcd}$\alpha_\mathrm{s}$,l.d=6,l.a=0}{v2}
% labels
\fmfv{l.a=150,l.d=4,l=$g$}{i1}
\fmfv{l.a=-150,l.d=4,l=$g$}{i2}
\fmfv{l.a=25,l=$\tau^-$}{o1}
\fmfv{l.a=-20,l=$\overline{\mathrm{b}}$}{o2}
\fmfv{l.a=25,l=$\tau^+$}{o3}
\fmfv{l.a=-20,l=\vspace{-2pt}b}{o4}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colqcd}{rgb}{1,0,0} % strong vertex (red)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(-6,14)(14,11){ % padding (L,T)(R,B)
\begin{fmfgraph*}(150,120) % dimensions (WH)
% line style
\fmfset{dash_len}{10} % dashes length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfleft{i2,i1}
\fmfright{o4,o3,o2,o1}
\fmfshift{12 down}{i1}
\fmfshift{12 up}{i2}
% internal vertices (exact placement)
\fmfforce{(.80w,.75h)}{lq1} % exact placement
\fmfforce{(.80w,.25h)}{lq2} % exact placement
% gg -> g
\fmf{gluon}{v1,i1}
\fmf{gluon}{i2,v1}
\fmf{gluon,t=1.1}{v1,v2} % s-channel
% g -> LQ LQ
\fmf{dashes,t=1.1,l.s=left,label=LQ}{v2,lq1}
\fmf{dashes,t=1.1,l.s=right,label=$\overline{\mathrm{LQ}}$}{v2,lq2}
% LQ -> ql
\fmf{fermion}{o2,lq1,o1}
\fmf{fermion}{o3,lq2,o4}
% vertex
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(1,,0,,0),
l=\strut\color{colqcd}$\alpha_\mathrm{s}$,l.d=6,l.a=0}{v2}
% labels
\fmfv{l.a=150,l.d=4,l=$g$}{i1}
\fmfv{l.a=-150,l.d=4,l=$g$}{i2}
\fmfv{l.a=25,l=$\tau^-$}{o1}
\fmfv{l.a=-20,l=$\overline{\mathrm{b}}$}{o2}
\fmfv{l.a=25,l=$\tau^+$}{o3}
\fmfv{l.a=-20,l=\vspace{-2pt}b}{o4}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
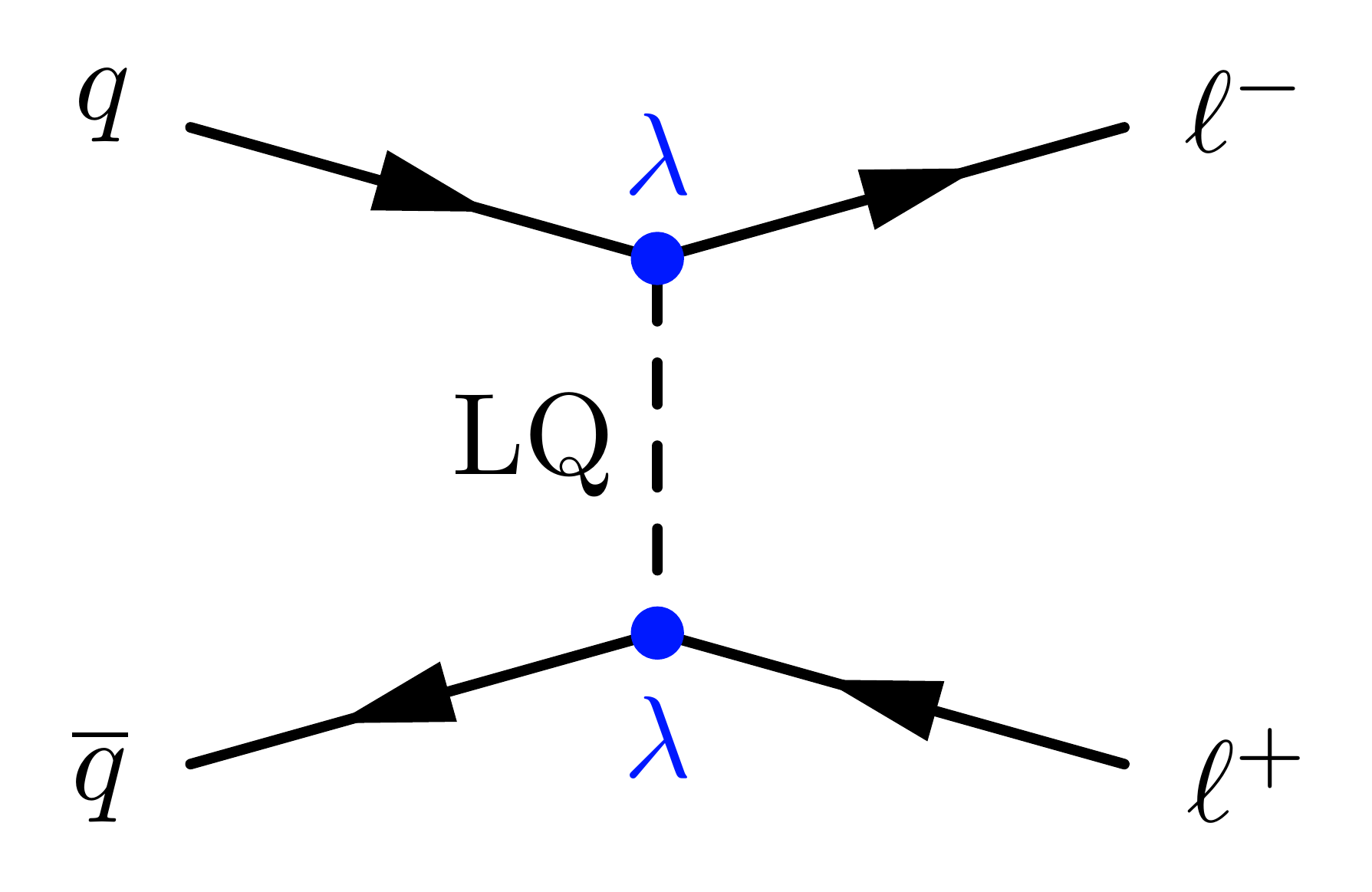
Nonresonant dilepton production through t-channel LQ exchange
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colvtx}{rgb}{0,.1,1} % LQ vertex (blue)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(-6,10)(3,10){ % padding (L,T)(R,B)
\begin{fmfgraph*}(110,60) % dimensions (WH)
% line style
\fmfset{dash_len}{10} % dashes length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfleft{i2,i1}
\fmfright{o2,o1}
% main: qq -> ll
\fmf{fermion}{i1,v1,o1}
\fmf{fermion}{o2,v2,i2}
\fmf{dashes,t=0.7,l.s=right,l.d=4,label=LQ}{v1,v2} % t-channel
% vertices
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}$\lambda$,l.d=6,l.a=90}{v1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}$\lambda$,l.d=6,l.a=-90}{v2}
% labels
\fmfv{l.a=160,l=$q$}{i1}
\fmfv{l.a=20,l=$\ell^-$}{o1}
\fmfv{l.a=-170,l=$\overline{q}$}{i2}
\fmfv{l.a=-10,l=$\ell^+$}{o2}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
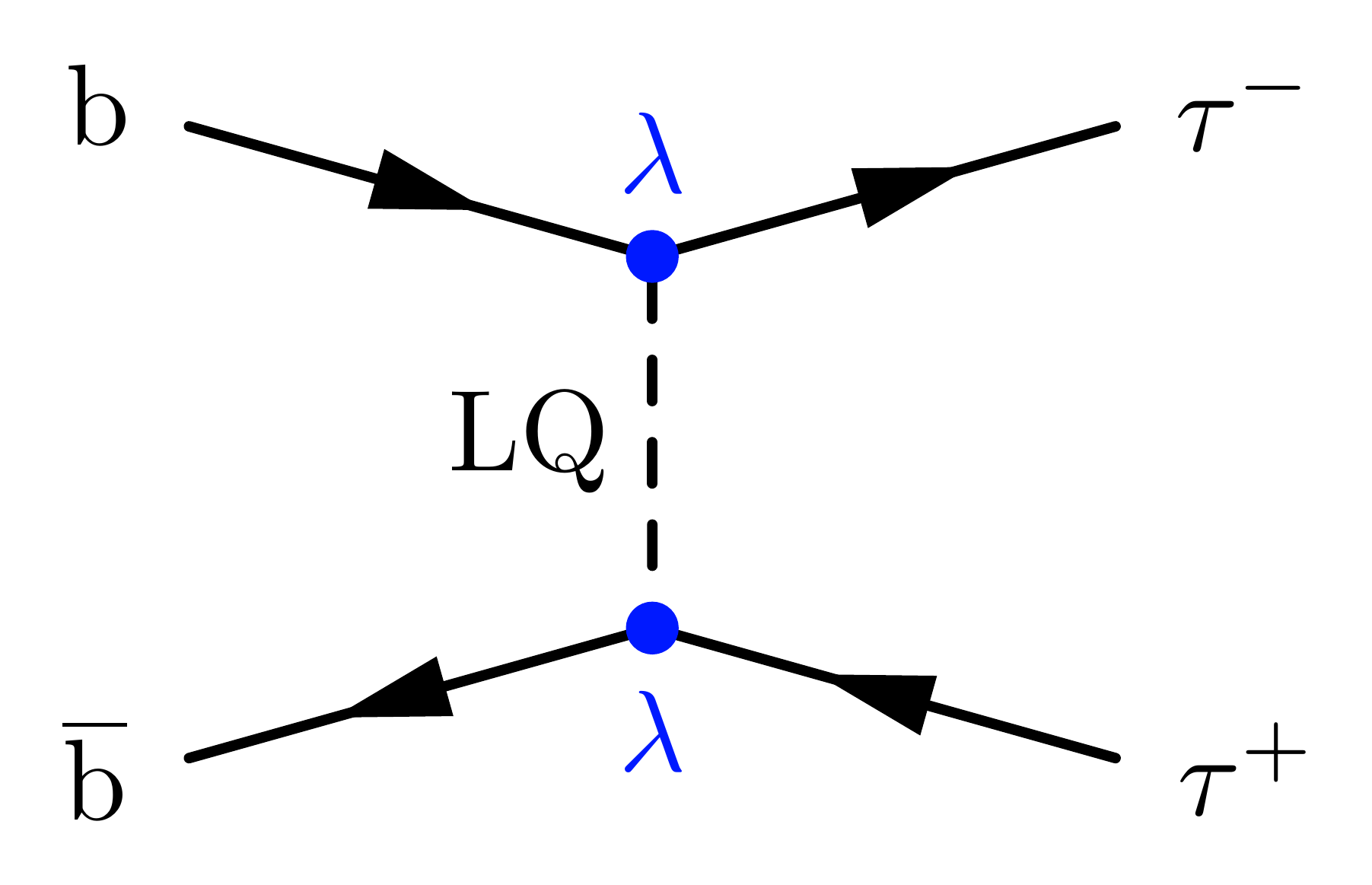
With two incoming bottoms quarks:
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colvtx}{rgb}{0,.1,1} % LQ vertex (blue)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(-6,10)(4,10){ % padding (L,T)(R,B)
\begin{fmfgraph*}(110,60) % dimensions (WH)
% line style
\fmfset{dash_len}{10} % dashes length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfleft{i2,i1}
\fmfright{o2,o1}
% main: qq -> ll
\fmf{fermion}{i1,v1,o1}
\fmf{fermion}{o2,v2,i2}
\fmf{dashes,t=0.7,l.s=right,l.d=4,label=LQ}{v1,v2} % t-channel
% vertices
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}$\lambda$,l.d=6,l.a=90}{v1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}$\lambda$,l.d=6,l.a=-90}{v2}
% labels
\fmfv{l.a=160,l=b}{i1}
\fmfv{l.a=20,l=$\tau^-$}{o1}
\fmfv{l.a=-170,l=$\overline{\mathrm{b}}$}{i2}
\fmfv{l.a=-10,l=$\tau^+$}{o2}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
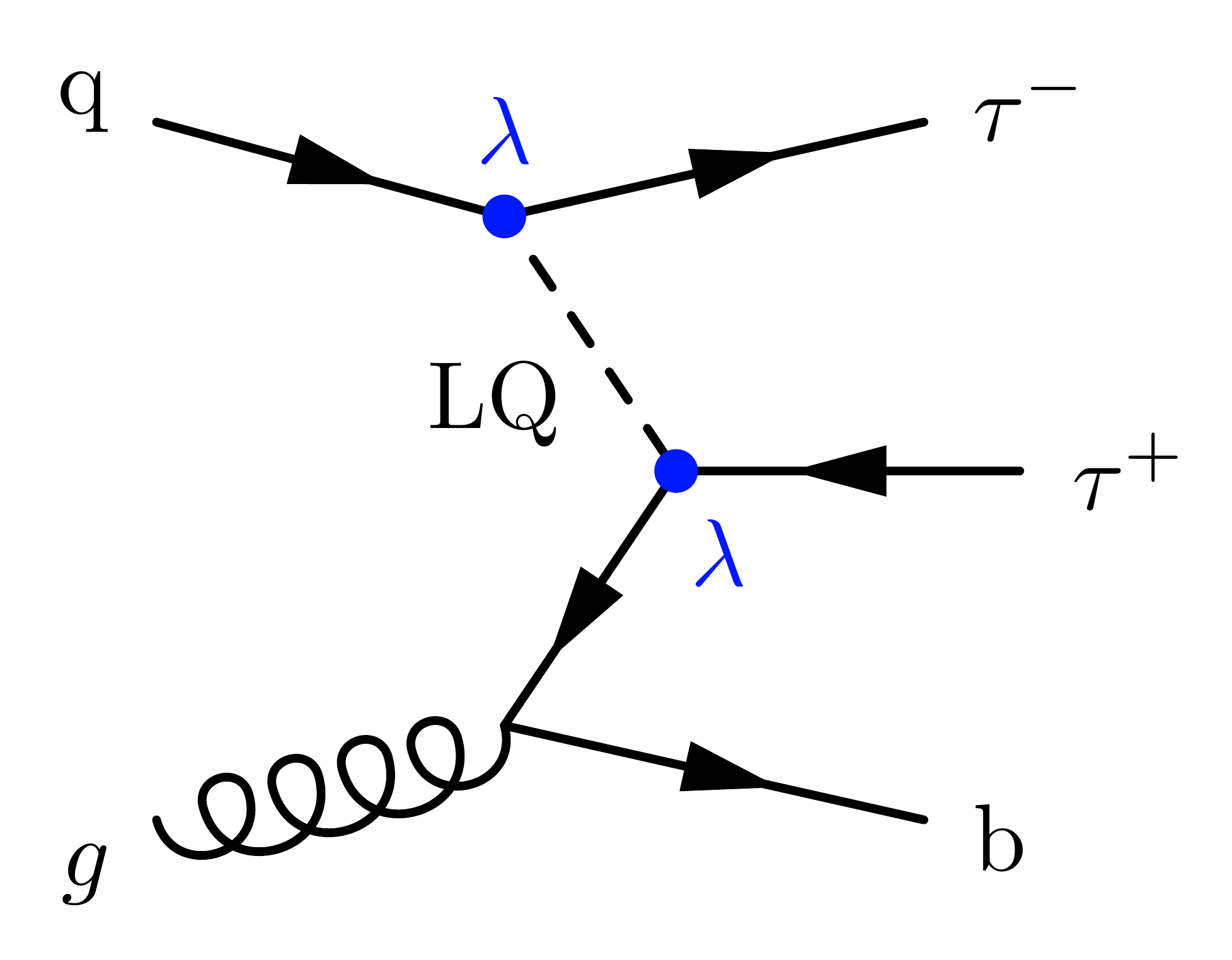
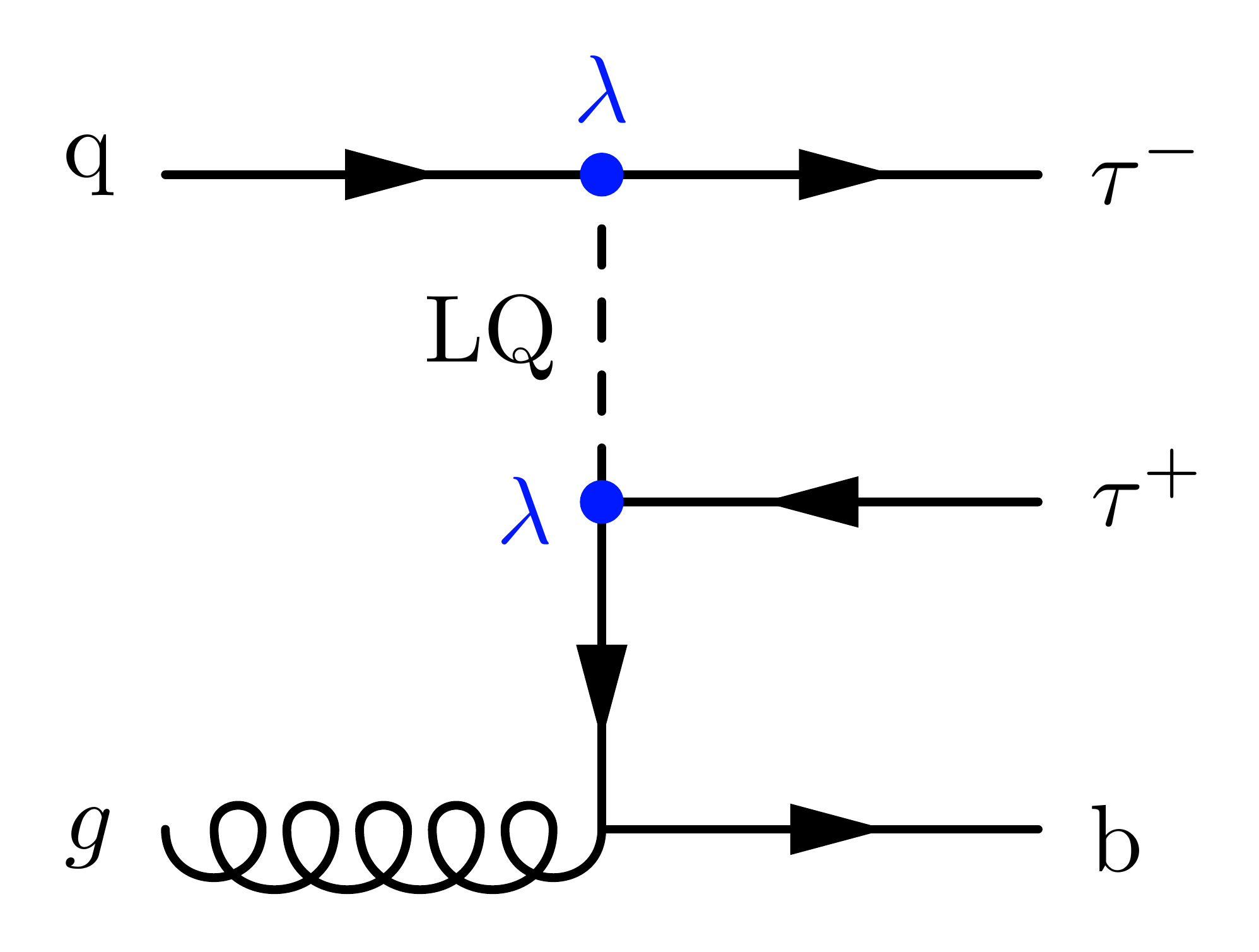
With one incoming bottom quark from gluon splitting, adding a bottom quark to the final state:
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colvtx}{rgb}{0,.1,1} % LQ vertex (blue)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(-6,12)(15,14){ % padding (L,T)(R,B)
\begin{fmfgraph*}(110,80) % dimensions (WH)
% line style
\fmfset{dash_len}{10} % dashes length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfleft{i2,i1}
\fmfright{o3,o2,o1}
% incoming
\fmf{fermion,t=1.7}{i1,v1}
\fmf{gluon,t=1.7}{i2,v2}
% t-channel
\fmf{dashes,l.s=left,l.d=4,label=LQ}{v,v1} % t-channel
\fmf{fermion}{v,v2} % t-channel
% outgoing
\fmf{fermion}{v1,o1}
\fmf{fermion}{v2,o3}
\fmf{fermion}{o2,v}
% vertices
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}$\lambda$,l.d=6,l.a=90}{v1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}\strut$\lambda$,l.d=4,l.a=-65}{v}
% labels
\fmfv{l.d=6,l.a=158,l=q}{i1}
\fmfv{l.d=6,l.a=-152,l=$g$}{i2}
\fmfv{l.d=6,l.a=22,l=$\tau^-$}{o1}
\fmfv{l.d=6,l.a=0,l=$\tau^+$}{o2}
\fmfv{l.d=6,l.a=-20,l=b}{o3}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colvtx}{rgb}{0,.1,1} % LQ vertex (blue)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(6,18)(16,12){ % padding (L,T)(R,B)
\begin{fmfgraph*}(100,75) % dimensions (WH)
% line style
\fmfset{dash_len}{10} % dashes length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfstraight
\fmfleft{i2,i1}
\fmfright{o3,o2,o1}
% main
\fmf{fermion}{i1,v1}
\fmf{fermion}{v1,o1}
\fmf{gluon}{i2,v2}
\fmf{fermion}{v2,o3}
\fmffreeze
\fmf{fermion}{v,v2} % t-channel
\fmf{dashes,l.s=left,l.d=5,label=LQ}{v,v1} % t-channel
\fmf{fermion,t=0}{o2,v} % tau out
% vertices
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}$\lambda$,l.d=6,l.a=90}{v1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}\strut$\lambda$,l.d=6,l.a=-160}{v}
% labels
\fmfv{l.d=6,l.a=170,l=q}{i1}
\fmfv{l.d=6,l.a=-170,l=$g$}{i2}
\fmfv{l.d=6,l.a=10,l=$\tau^-$}{o1}
\fmfv{l.d=6,l.a=0,l=\strut$\tau^+$}{o2}
\fmfv{l.d=6,l.a=-10,l=b}{o3}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
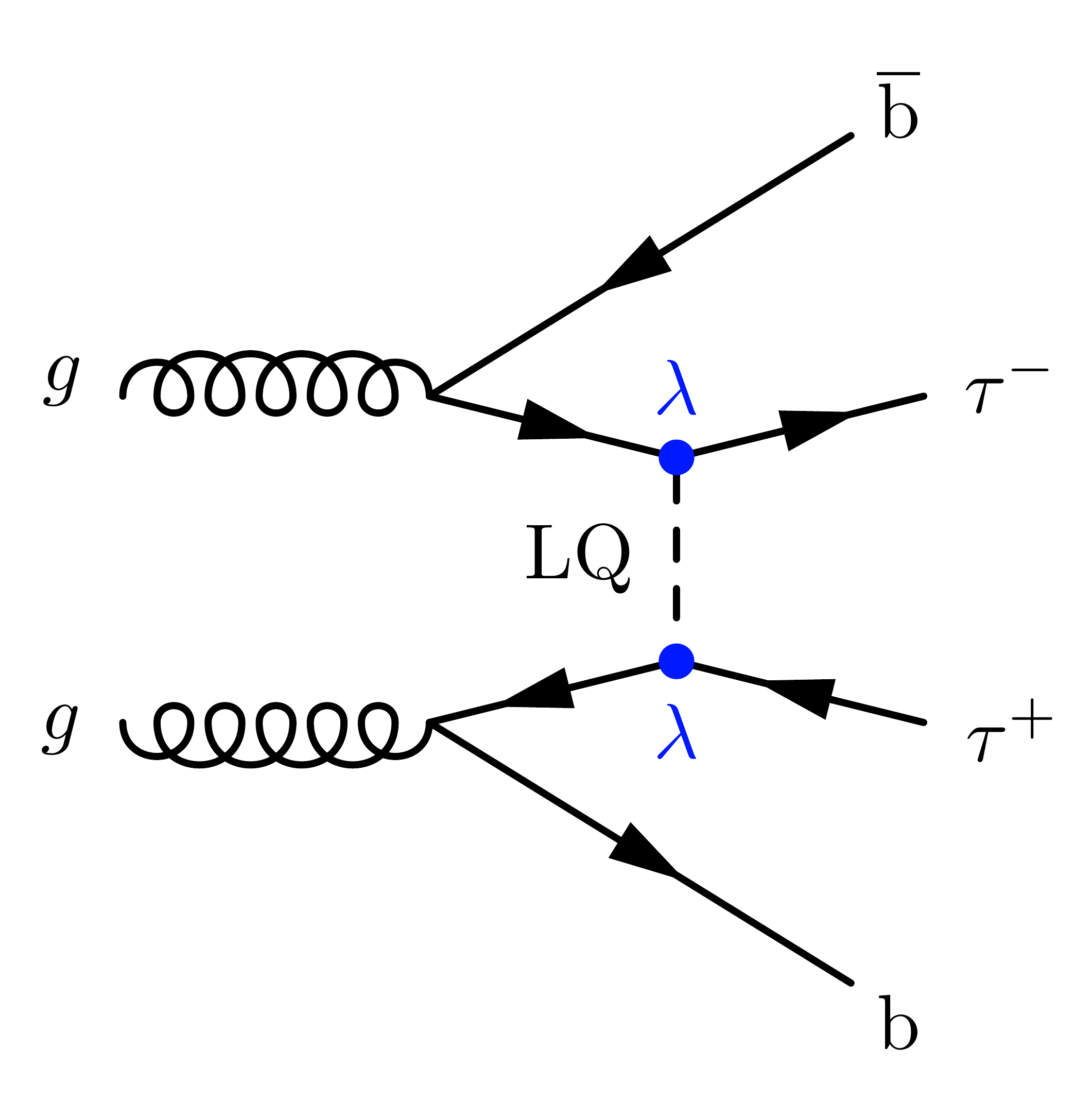
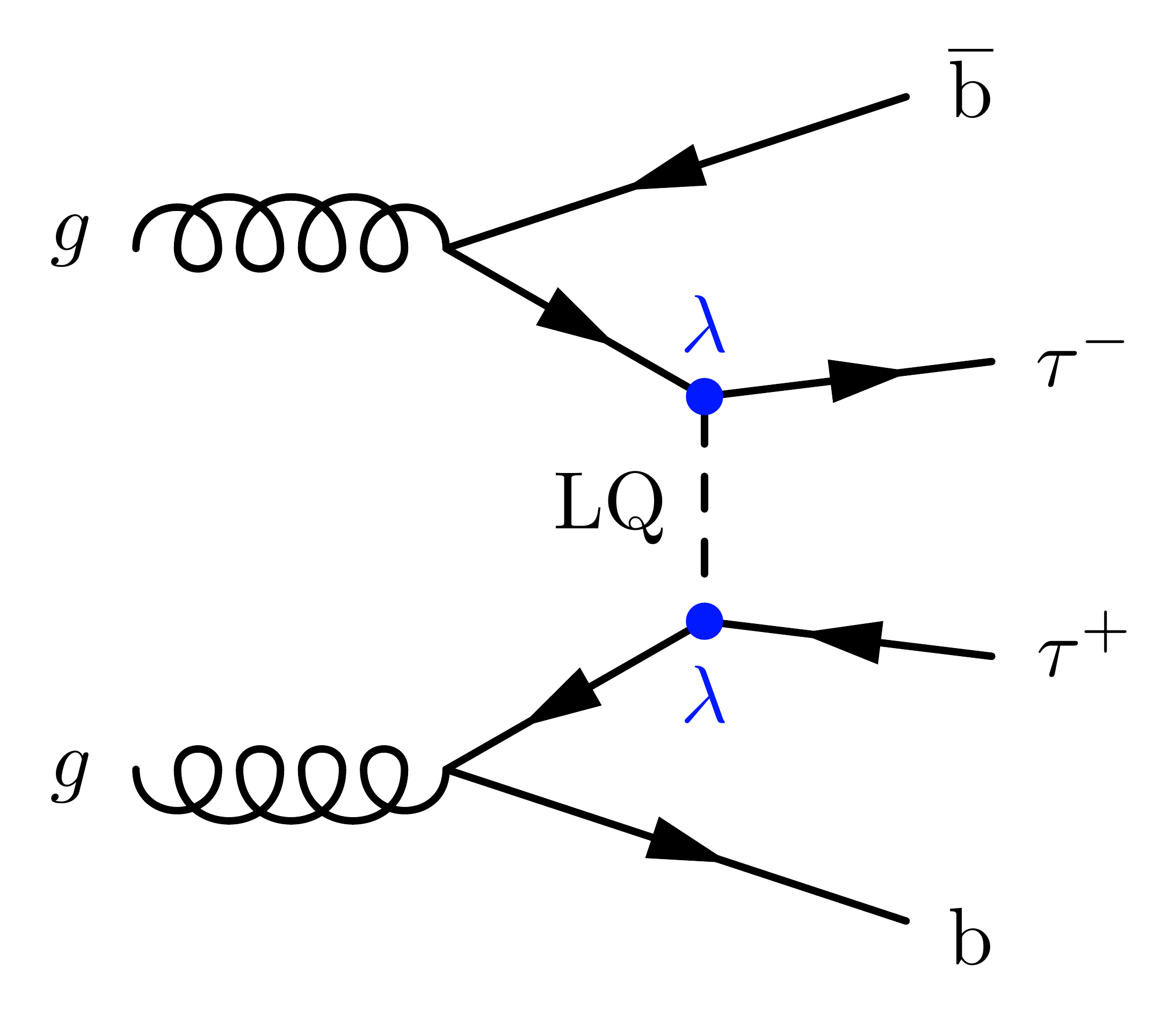
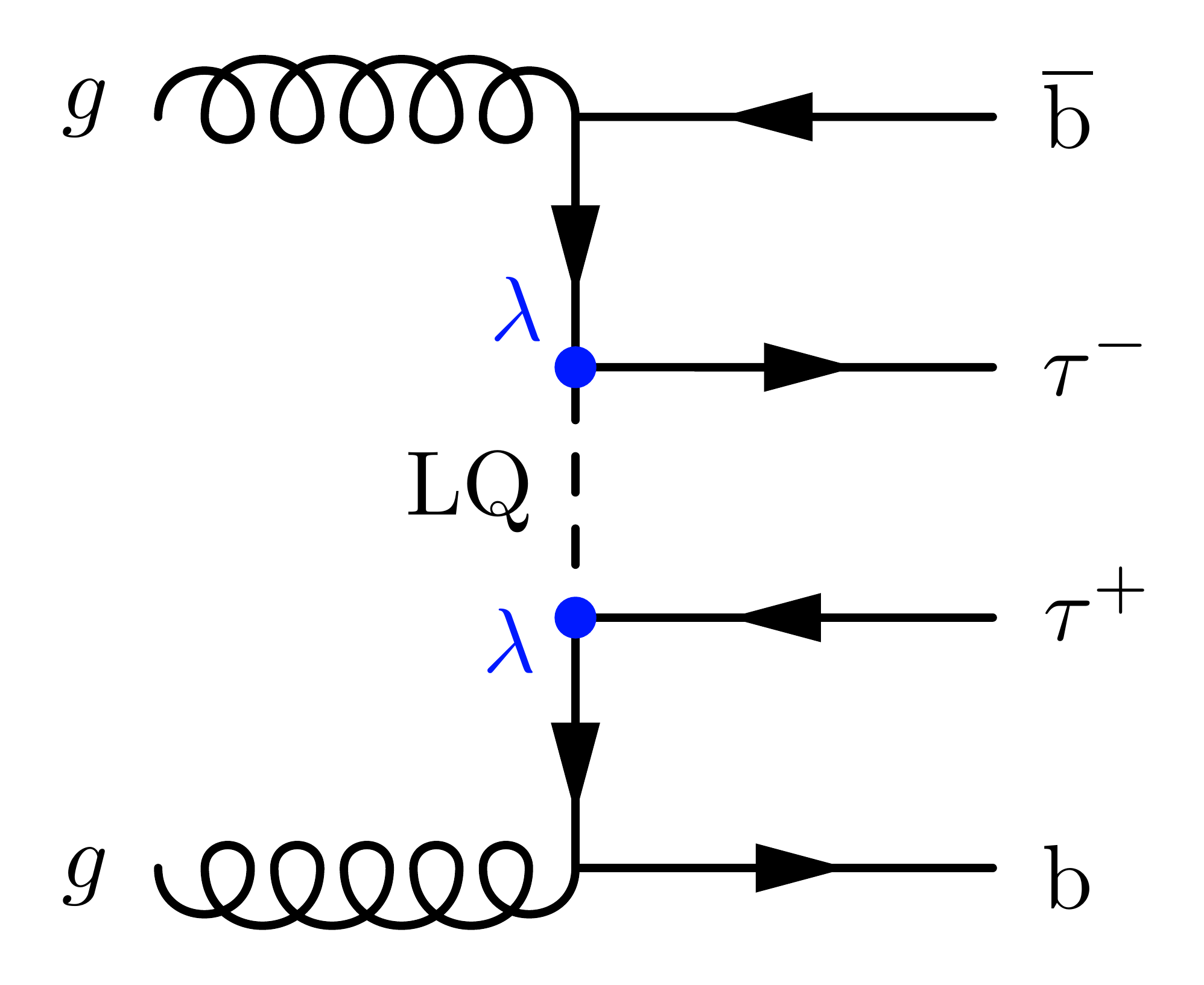
With both incoming bottom quarks from gluon splitting, adding two bottom quarks to the final state:
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colvtx}{rgb}{0,.1,1} % LQ vertex (blue)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(3,9)(13,9){ % padding (L,T)(R,B)
\begin{fmfgraph*}(115,135) % dimensions (WH)
% line style
\fmfset{dash_len}{10} % dashes length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfleft{d,i2,i1,d}
\fmfright{b2,o2,o1,b1}
\fmfshift{8 down}{b1}
\fmfshift{8 up}{b2}
% gluon splitting
\fmf{gluon}{g1,i1}
\fmf{gluon}{i2,g2}
\fmf{phantom,t=0.62}{g1,o1,o2,g2} % pull gluons straight right
\fmffreeze
% main: qq -> ll
\fmf{fermion}{g1,v1,o1}
\fmf{fermion}{o2,v2,g2}
\fmf{fermion}{b1,g1}
\fmf{fermion}{g2,b2}
\fmf{dashes,t=0.6,l.s=right,label=LQ}{v1,v2} % t-channel
% vertices
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}$\lambda$,l.d=6,l.a=90}{v1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}$\lambda$,l.d=6,l.a=-90}{v2}
% labels
\fmfv{l.a=160,l=$g$}{i1}
\fmfv{l.a=-170,l=$g$}{i2}
\fmfv{l.a=20,l=$\tau^-$}{o1}
\fmfv{l.a=-10,l=$\tau^+$}{o2}
\fmfv{l.a=25,l.d=4,l=\vspace{-2pt}$\overline{\mathrm{b}}$}{b1}
\fmfv{l.a=-25,l.d=4,l=b}{b2}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colvtx}{rgb}{0,.1,1} % LQ vertex (blue)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(1,4)(15,4){ % padding (L,T)(R,B)
\begin{fmfgraph*}(120,125) % dimensions (WH)
% line style
\fmfset{dash_len}{10} % dashes length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfleft{d,i2,m2,m1,i1,d} % add dummies 'd' for spacing
\fmfright{b2,p2,o2,o1,p1,b1} % add dummies 'd' for spacing
\fmfshift{3 down}{i1,p1}
\fmfshift{3 up}{i2,p2}
\fmfshift{7 down}{b1,o2}
\fmfshift{7 up}{b2,o1}
% incoming
\fmf{gluon}{v1,i1}
\fmf{gluon}{i2,v2}
\fmf{phantom,t=0.6}{v1,p1,p2,v2} % pull gluons straight right
\fmffreeze
%%%% outgoing tau leptons
%%%\fmf{fermion}{lq1,o1} % tau out
%%%\fmf{fermion}{o2,lq2} % tau out
%%%\fmf{phantom,t=0.5}{lq1,m1,m2,lq2} % pull taus straight left
%%%\fmffreeze
%%% outgoing b quarks from gluon splitting
\fmf{fermion}{b1,v1}
\fmf{fermion}{v2,b2}
% t-channel
\fmf{fermion}{v1,lq1} % t-channel
\fmf{dashes,t=0.8,l.s=right,l.d=5,label=LQ}{lq1,lq2} % t-channel
\fmf{fermion}{lq2,v2} % t-channel
% outgoing tau leptons
\fmf{fermion,t=0.9}{lq1,o1} % tau out
\fmf{fermion,t=0.9}{o2,lq2} % tau out
% vertices
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}$\lambda$,l.d=6,l.a=90}{lq1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}$\lambda$,l.d=6,l.a=-90}{lq2}
% labels
\fmfv{l.d=6,l.a=170,l=$g$}{i1}
\fmfv{l.d=6,l.a=-170,l=$g$}{i2}
\fmfv{l.d=6,l.a=10,l=$\tau^-$}{o1}
\fmfv{l.d=6,l.a=0,l=\strut$\tau^+$}{o2}
\fmfv{l.d=6,l.a=20,l=$\overline{\mathrm{b}}$}{b1}
\fmfv{l.d=6,l.a=-20,l=b}{b2}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colvtx}{rgb}{0,.1,1} % LQ vertex (blue)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(6,12)(16,12){ % padding (L,T)(R,B)
\begin{fmfgraph*}(100,90) % dimensions (WH)
% line style
\fmfset{dash_len}{10} % dashes length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfstraight
\fmfleft{i2,i1}
\fmfright{b2,o2,o1,b1}
% incoming
\fmf{gluon}{v1,i1}
\fmf{gluon}{i2,v2}
% outgoing b quarks from gluon splitting
\fmf{fermion}{b1,v1}
\fmf{fermion}{v2,b2}
\fmffreeze
% t-channel
\fmf{fermion}{v1,lq1} % t-channel
\fmf{dashes,l.s=right,l.d=5,label=LQ}{lq1,lq2} % t-channel
\fmf{fermion}{lq2,v2} % t-channel
\fmffreeze
% outgoing tau leptons
\fmf{fermion}{lq1,o1} % tau out
\fmf{fermion}{o2,lq2} % tau out
% vertices
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}$\lambda$,l.d=5,l.a=140}{lq1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=(0,,.1,,1),
l=\color{colvtx}\vspace{-2pt}$\lambda$,l.d=5,l.a=-160}{lq2}
% labels
\fmfv{l.d=6,l.a=170,l=$g$}{i1}
\fmfv{l.d=6,l.a=-170,l=$g$}{i2}
\fmfv{l.d=6,l.a=10,l=$\tau^-$}{o1}
\fmfv{l.d=6,l.a=0,l=\strut$\tau^+$}{o2}
\fmfv{l.d=6,l.a=10,l=$\overline{\mathrm{b}}$}{b1}
\fmfv{l.d=6,l.a=-10,l=b}{b2}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
Full code
The LaTeX code below collects all the diagrams above into one big file that produces a multipage PDF. Please find download links below, or edit and compile here if you like:
% !TEX program = pdflatexmk
% !TEX parameter = -shell-escape
% Author: Izaak Neutelings (September 2024)
% Instructions: To compile via command line, run the following twice
% pdflatex -shell-escape LQ.tex
\documentclass[11pt,border=2pt,multi=page,crop]{standalone}
\usepackage{feynmp-auto}
% DEFINE TEXT COLORS
\usepackage{xcolor}
\definecolor{colvtx}{rgb}{0,.1,1} % LQ vertex (blue)
\definecolor{colqcd}{rgb}{1,0,0} % strong vertex (red)
% DEFINE COLOR MACROS
% The following loops over the user color names and defines
% a handy \<colname> command to set text color, as well as
% defines colors in MetaPost of the same and value for lines
\usepackage{pgffor} % for \foreach
\def\MPcolors{} % MetaPost code importing xcolor names
\foreach \colname in {colvtx,colqcd}{ % create command & MetaPost code
\expandafter\xdef\csname\colname\endcsname{\noexpand\color{\colname}} % \newcommand\<colname>
\convertcolorspec{named}{\colname}{rgb}\tmprgb % get rgb code
\xdef\MPcolors{\MPcolors color \colname; \colname := (\tmprgb); } % add color name
}
% DEFINE fmfpicture ENVIRONMENT
\usepackage{environ} % for \NewEnviron
\NewEnviron{fmfpicture}[3]{%
\begin{page} % to create standalone page
\fmfframe(#1)(#2){ % padding (LT)(RB)
\begin{fmffile}{feynmp-#3} % auxiliary files (use unique name!)
\fmfset{dash_len}{10} % dashes length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
\fmfcmd\MPcolors % define custom line colors in MetaPost
\BODY % main code
\end{fmffile}
}
\end{page}
}
\begin{document}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%% SINGLE LQ PRODUCTION %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% SINGLE LQ PRODUCTION - s-channel
\begin{fmfpicture}{3,22}{13,15}{LQ_single_schan} % padding (LTRB)
\begin{fmfgraph*}(130,80) % dimensions (WH)
% external vertices
\fmfstraight
\fmfleft{i2,i1}
\fmfright{o3,o2,o1}
\fmfshift{8 up}{o1,o2}
\fmfshift{18 left}{o3}
% internal vertices (exact placement)
\fmfforce{(.22w,.50h)}{v1} % exact placement
\fmfforce{(.62w,.50h)}{v2} % exact placement
\fmfforce{(.78w,.86h)}{lq} % exact placement
% incoming partons
\fmf{gluon}{v1,i1}
\fmf{fermion}{i2,v1}
% s-channel
\fmf{fermion,l.s=right,label=$q$}{v1,v2}
% associated lepton
\fmf{fermion}{v2,o3}
% LQ -> lepton + quark
\fmf{dashes,t=1.2,l.s=left,label=LQ}{v2,lq}
\fmf{fermion}{o2,lq,o1}
% vertex
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx$\lambda$,l.d=6,l.a=-8}{v2}
% labels
\fmfv{l.a=155,l.d=4,l=$g$}{i1}
\fmfv{l.a=-155,l.d=4,l=$q$}{i2}
\fmfv{l.a=25,l.d=4,l=$q$}{o1}
\fmfv{l.a=-20,l.d=4,l=\vspace{-2pt}$\ell^+$}{o2}
\fmfv{l.a=-25,l.d=3,l=$\ell^-$}{o3}
\end{fmfgraph*}
\end{fmfpicture}
% SINGLE LQ PRODUCTION - s-channel
\begin{fmfpicture}{3,22}{13,13}{LQ_single_schan_btautau} % padding (LTRB)
\begin{fmfgraph*}(130,80) % dimensions (WH)
% external vertices
\fmfstraight
\fmfleft{i2,i1}
\fmfright{o3,o2,o1}
\fmfshift{8 up}{o1,o2}
\fmfshift{18 left}{o3}
% internal vertices (exact placement)
\fmfforce{(.22w,.50h)}{v1} % exact placement
\fmfforce{(.62w,.50h)}{v2} % exact placement
\fmfforce{(.78w,.86h)}{lq} % exact placement
% incoming partons
\fmf{gluon}{v1,i1}
\fmf{fermion}{i2,v1}
% s-channel
\fmf{fermion,l.s=right,label=b}{v1,v2}
% associated lepton
\fmf{fermion}{v2,o3}
% LQ -> lepton + quark
\fmf{dashes,t=1.2,l.s=left,label=LQ}{v2,lq}
\fmf{fermion}{o2,lq,o1}
% vertex
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx$\lambda$,l.d=6,l.a=-8}{v2}
% labels
\fmfv{l.a=155,l.d=4,l=$g$}{i1}
\fmfv{l.a=-155,l.d=4,l=b}{i2}
\fmfv{l.a=25,l.d=4,l=b}{o1}
\fmfv{l.a=-20,l.d=4,l=\vspace{-2pt}$\tau^+$}{o2}
\fmfv{l.a=-20,l.d=5,l=\vspace{-2pt}$\tau^-$}{o3}
\end{fmfgraph*}
\end{fmfpicture}
% SINGLE LQ PRODUCTION - s-channel, gluon-splitting
\begin{fmfpicture}{3,32}{13,13}{LQ_single_schan_gsplit} % padding (LTRB)
\begin{fmfgraph*}(135,95) % dimensions (WH)
% external vertices
\fmfstraight
\fmfleft{i2,i1}
\fmfright{o4,o3,o2,o1}
\fmfshift{20 up}{o1,o2}
\fmfshift{8 up}{o3}
\fmfshift{6 left}{o3}
\fmfshift{28 left}{o4}
% internal vertices (exact placement)
\fmfforce{(.25w,.31h)}{vg} % exact placement
\fmfforce{(.25w,.69h)}{v1} % exact placement
\fmfforce{(.62w,.69h)}{v2} % exact placement
\fmfforce{(.78w,1.04h)}{lq} % exact placement
% gluon splitting
\fmf{gluon}{v1,i1}
\fmf{gluon}{i2,vg}
\fmf{fermion,l.s=left,label=b}{vg,v1}
\fmf{fermion}{o4,vg}
% s-channel
\fmf{fermion,l.s=left,label=b}{v1,v2}
% associated lepton
\fmf{fermion}{v2,o3}
% LQ -> lepton + quark
\fmf{dashes,t=1.2,l.d=4,l.s=left,label=LQ}{v2,lq}
\fmf{fermion}{o2,lq,o1}
% vertex
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx$\lambda$,l.d=6,l.a=-110}{v2}
% labels
\fmfv{l.a=155,l.d=4,l=$g$}{i1}
\fmfv{l.a=-155,l.d=4,l=b}{i2}
\fmfv{l.a=25,l.d=4,l=b}{o1}
\fmfv{l.a=-20,l.d=4,l=\vspace{-2pt}$\tau^+$}{o2}
\fmfv{l.a=-20,l.d=5,l=\vspace{-2pt}$\tau^-$}{o3}
\fmfv{l.a=-20,l.d=5,l=\vspace{-2pt}b}{o4}
\end{fmfgraph*}
\end{fmfpicture}
% SINGLE LQ PRODUCTION - s-channel, gluon-splitting
\begin{fmfpicture}{-10,14}{12,11}{LQ_single_schan_gsplit2} % padding (LTRB)
\begin{fmfgraph*}(130,90) % dimensions (WH)
% external vertices
\fmfleft{i2,i1}
\fmfright{o4,o3,o2,o1}
\fmfshift{12 down}{i1}
\fmfshift{12 up}{i2}
% gluon splitting
\fmf{gluon}{v1,i1}
\fmf{gluon}{i2,v2}
\fmf{fermion,t=0.9,l.s=left,label=b}{v2,v1} % t-channel
\fmf{phantom,t=0.6}{v1,o1,o4,v2}
\fmffreeze
% outgoing bottom quarks
\fmf{fermion}{v1,lq1}
\fmf{fermion,t=0.8}{lq1,o1}
\fmf{fermion}{o4,v2}
\fmffreeze
% LQ -> btau
\fmf{dashes,t=0.9,l.s=right,l.d=4,label=LQ}{lq1,lq2}
\fmf{fermion,t=0.9}{o2,lq2,o3}
\fmf{phantom,t=0.9}{v2,lq2}
% vertex
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx$\lambda$,l.d=6,l.a=120}{lq1}
% labels
\fmfv{l.a=160,l.d=4,l=$g$}{i1}
\fmfv{l.a=-160,l.d=4,l=$g$}{i2}
\fmfv{l.a=25,l.d=4,l=$\tau^-$}{o1}
\fmfv{l.a=25,l.d=4,l=\vspace{-2pt}$\tau^+$}{o2}
\fmfv{l.a=-20,l.d=5,l=b}{o3}
\fmfv{l.a=-20,l.d=5,l=\vspace{-2pt}b}{o4}
\end{fmfgraph*}
\end{fmfpicture}
% SINGLE LQ PRODUCTION - t-channel
\begin{fmfpicture}{3,15}{13,11}{LQ_single_tchan} % padding (LTRB)
\begin{fmfgraph*}(110,80) % dimensions (WH)
% external vertices
\fmfstraight
\fmfleft{i2,i1}
\fmfright{o3,o2,o1}
\fmfshift{20 left}{o3}
% internal vertices (exact placement)
\fmfforce{(.34w,.75h)}{v1} % exact placement
\fmfforce{(.34w,.23h)}{v2} % exact placement
\fmfforce{(.73w,.75h)}{lq} % exact placement
\fmffreeze
% gluon + quarks
\fmf{gluon}{v1,i1}
\fmf{fermion}{i2,v2,o3}
% LQs
\fmf{dashes,t=1.2,l.s=left,l.d=4,label=LQ}{v1,lq}
\fmf{dashes,l.s=left,l.d=4,label=LQ}{v2,v1}
% LQ -> lepton + quark
\fmf{fermion}{o2,lq,o1}
% vertex
%\fmfv{d.sh=circle,d.f=full,d.si=4,f=colqcd,
% l=\colqcd$\alpha_\mathrm{s}$,l.d=5,l.a=-40}{v1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx$\lambda$,l.d=7,l.a=-90}{v2}
% labels
\fmfv{l.a=150,l.d=4,l=$g$}{i1}
\fmfv{l.a=-160,l.d=4,l=b}{i2}
\fmfv{l.a=-20,l.d=5,l=$\tau^-$}{o3}
\fmfv{l.a=25,l.d=4,l=b}{o1}
\fmfv{l.a=-20,l.d=5,l=$\tau^+$}{o2}
\end{fmfgraph*}
\end{fmfpicture}
% SINGLE LQ PRODUCTION - t-channel (photon-induced)
\begin{fmfpicture}{3,15}{13,11}{LQ_single_tchan_photon} % padding (LTRB)
\begin{fmfgraph*}(110,80) % dimensions (WH)
% external vertices
\fmfstraight
\fmfleft{i2,i1}
\fmfright{o3,o2,o1}
\fmfshift{20 left}{o3}
% internal vertices (exact placement)
\fmfforce{(.34w,.75h)}{v1} % exact placement
\fmfforce{(.34w,.23h)}{v2} % exact placement
\fmfforce{(.73w,.75h)}{lq} % exact placement
\fmffreeze
% gluon + quarks
\fmf{fermion}{i1,v1}
\fmf{photon}{i2,v2} % photon
\fmf{fermion}{v2,o3}
% LQs
\fmf{dashes,t=1.2,l.s=left,l.d=4,label=LQ}{v1,lq}
\fmf{fermion,l.s=right,label=$\tau$}{v1,v2}
% LQ -> lepton + quark
\fmf{fermion}{o2,lq,o1}
% vertex
%\fmfv{d.sh=circle,d.f=full,d.si=4,f=colqcd,
% l=\colqcd$\alpha_\mathrm{s}$,l.d=5,l.a=-40}{v1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx$\lambda$,l.d=7,l.a=-90}{v2}
% labels
\fmfv{l.a=150,l.d=4,l=$g$}{i1}
\fmfv{l.a=-160,l.d=4,l=$\gamma$}{i2}
\fmfv{l.a=-20,l.d=5,l=$\tau^-$}{o3}
\fmfv{l.a=25,l.d=4,l=b}{o1}
\fmfv{l.a=-20,l.d=5,l=$\tau^+$}{o2}
\end{fmfgraph*}
\end{fmfpicture}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%% LQ PAIR PRODUCTION %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% LQ PAIR PRODUCTION - gluon fusion, s-channel
\begin{fmfpicture}{-8,16}{6,17}{LQ_pair_gg_schan} % padding (LTRB)
\begin{fmfgraph*}(120,70) % dimensions (WH)
% external vertices
\fmfleft{i2,i1}
\fmfright{o2,o1}
% gg -> g
\fmf{gluon}{i2,v1,i1}
\fmf{gluon,t=1.1}{v1,v2} % s-channel
% g -> LQ LQ
\fmf{dashes,t=1.2}{o1,v2}
\fmf{dashes,t=1.2}{o2,v2}
% vertex
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colqcd,
l=\strut\colqcd$\alpha_\mathrm{s}$,l.d=6,l.a=0}{v2}
% labels
\fmfv{l.a=150,l.d=4,l=$g$}{i1}
\fmfv{l.a=-150,l.d=4,l=$g$}{i2}
\fmfv{l.a=25,l.d=3,l=LQ}{o1}
\fmfv{l.a=-25,l.d=4,l=$\overline{\mathrm{LQ}}$}{o2}
\end{fmfgraph*}
\end{fmfpicture}
% LQ PAIR PRODUCTION - quark-antiquark annihilation
\begin{fmfpicture}{-10,16}{4,17}{LQ_pair_qq} % padding (LTRB)
\begin{fmfgraph*}(120,70) % dimensions (WH)
% external vertices
\fmfleft{i2,i1}
\fmfright{o2,o1}
% gg -> g
\fmf{fermion}{i1,v1,i2}
\fmf{gluon,t=1.1}{v2,v1} % s-channel
% g -> LQ LQ
\fmf{dashes,t=1.2}{o1,v2}
\fmf{dashes,t=1.2}{o2,v2}
% vertex
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colqcd,
l=\strut\colqcd$\alpha_\mathrm{s}$,l.d=6,l.a=0}{v2}
% labels
\fmfv{l.a=150,l.d=4,l=$q$}{i1}
\fmfv{l.a=-150,l.d=4,l=$\overline{q}$}{i2}
\fmfv{l.a=25,l.d=3,l=LQ}{o1}
\fmfv{l.a=-25,l.d=4,l=$\overline{\mathrm{LQ}}$}{o2}
\end{fmfgraph*}
\end{fmfpicture}
% LQ PAIR PRODUCTION - gluon-LQ fusion
\begin{fmfpicture}{-8,16}{6,17}{LQ_pair_ggLQ} % padding (LTRB)
\begin{fmfgraph*}(80,60) % dimensions (WH)
% external vertices
\fmfleft{i2,i1}
\fmfright{o2,o1}
% gg -> g
\fmf{gluon}{i2,v,i1}
% g -> LQ LQ
\fmf{dashes,t=1.2}{o1,v}
\fmf{dashes,t=1.2}{o2,v}
% vertex
%\fmfv{d.sh=circle,d.f=full,d.si=4,f=colqcd,
% l=\strut\colqcd$\alpha_\mathrm{s}$,l.d=6,l.a=0}{v}
% labels
\fmfv{l.a=150,l.d=4,l=$g$}{i1}
\fmfv{l.a=-150,l.d=4,l=$g$}{i2}
\fmfv{l.a=25,l.d=4,l=LQ}{o1}
\fmfv{l.a=-25,l.d=5,l=$\overline{\mathrm{LQ}}$}{o2}
\end{fmfgraph*}
\end{fmfpicture}
% LQ PAIR PRODUCTION - gluon fusion, t-channel
\begin{fmfpicture}{-10,13}{4,13}{LQ_pair_gg_tchan} % padding (LTRB)
\begin{fmfgraph*}(120,70) % dimensions (WH)
% external vertices
\fmfleft{i2,i1}
\fmfright{o2,o1}
% gg -> LQ LQ
\fmf{gluon}{v1,i1}
\fmf{gluon}{i2,v2}
\fmf{dashes,t=0.8,l.s=right,label=LQ}{v1,v2} % t-channel
% outgoing LQs
\fmf{dashes}{o1,v1}
\fmf{dashes}{o2,v2}
% vertices
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colqcd,
l=\colqcd$\alpha_\mathrm{s}$,l.d=8,l.a=70}{v1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colqcd,
l=\colqcd$\alpha_\mathrm{s}$,l.d=8,l.a=-70}{v2}
% labels
\fmfv{l.a=150,l.d=4,l=$g$}{i1}
\fmfv{l.a=-150,l.d=4,l=$g$}{i2}
\fmfv{l.a=20,l.d=5,l=LQ}{o1}
\fmfv{l.a=-20,l.d=5,l=$\overline{\mathrm{LQ}}$}{o2}
\end{fmfgraph*}
\end{fmfpicture}
% LQ PAIR PRODUCTION - quark-antiquark annihilation, t-channel
\begin{fmfpicture}{-10,11}{4,11}{LQ_pair_qq_tchan} % padding (LTRB)
\begin{fmfgraph*}(120,70) % dimensions (WH)
% external vertices
\fmfleft{i2,i1}
\fmfright{o2,o1}
% qq -> LQ LQ
\fmf{fermion}{i1,v1}
\fmf{fermion}{v2,i2}
\fmf{fermion,t=0.8,l.s=right,label=$\ell$}{v1,v2} % t-channel
% outgoing LQs
\fmf{dashes}{o1,v1}
\fmf{dashes}{o2,v2}
% vertices
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx$\lambda$,l.d=7,l.a=90}{v1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx$\lambda$,l.d=7,l.a=-90}{v2}
% labels
\fmfv{l.a=160,l.d=4,l=$q$}{i1}
\fmfv{l.a=-160,l.d=4,l=$\overline{q}$}{i2}
\fmfv{l.a=20,l.d=4,l=LQ}{o1}
\fmfv{l.a=-20,l.d=5,l=$\overline{\mathrm{LQ}}$}{o2}
\end{fmfgraph*}
\end{fmfpicture}
% LQ PAIR PRODUCTION
\begin{fmfpicture}{3,14}{14,11}{LQ_pair_gg_decay} % padding (LTRB)
\begin{fmfgraph*}(140,100) % dimensions (WH)
% external vertices
\fmfstraight
\fmfleft{i2,i1}
\fmfright{o4,o3,o2,o1}
\fmfshift{10 down}{i1}
\fmfshift{10 up}{i2}
% internal vertices (exact placement)
\fmfforce{(.80w,.82h)}{lq1} % exact placement
\fmfforce{(.80w,.18h)}{lq2} % exact placement
% gg -> g
\fmf{gluon}{v1,i1}
\fmf{gluon}{i2,v1}
\fmf{gluon,t=1.1}{v1,v2} % s-channel
% g -> LQ LQ
\fmf{dashes,t=1.2,l.s=left,label=LQ}{v2,lq1}
\fmf{dashes,t=1.2,l.s=right,label=$\overline{\mathrm{LQ}}$}{v2,lq2}
% LQ -> ql
\fmf{fermion}{o2,lq1,o1}
\fmf{fermion}{o3,lq2,o4}
% vertex
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colqcd,
l=\strut\colqcd$\alpha_\mathrm{s}$,l.d=6,l.a=0}{v2}
% labels
\fmfv{l.a=150,l.d=4,l=$g$}{i1}
\fmfv{l.a=-150,l.d=4,l=$g$}{i2}
\fmfv{l.a=25,l=$\tau^-$}{o1}
\fmfv{l.a=-20,l=$\overline{\mathrm{b}}$}{o2}
\fmfv{l.a=25,l=$\tau^+$}{o3}
\fmfv{l.a=-20,l=\vspace{-2pt}b}{o4}
\end{fmfgraph*}
\end{fmfpicture}
% LQ PAIR PRODUCTION - round
\begin{fmfpicture}{-6,14}{14,11}{LQ_pair_gg_decay_round} % padding (LTRB)
\begin{fmfgraph*}(150,120) % dimensions (WH)
% external vertices
\fmfleft{i2,i1}
\fmfright{o4,o3,o2,o1}
\fmfshift{12 down}{i1}
\fmfshift{12 up}{i2}
% internal vertices (exact placement)
\fmfforce{(.80w,.75h)}{lq1} % exact placement
\fmfforce{(.80w,.25h)}{lq2} % exact placement
% gg -> g
\fmf{gluon}{v1,i1}
\fmf{gluon}{i2,v1}
\fmf{gluon,t=1.1}{v1,v2} % s-channel
% g -> LQ LQ
\fmf{dashes,t=1.1,l.s=left,label=LQ}{v2,lq1}
\fmf{dashes,t=1.1,l.s=right,label=$\overline{\mathrm{LQ}}$}{v2,lq2}
% LQ -> ql
\fmf{fermion}{o2,lq1,o1}
\fmf{fermion}{o3,lq2,o4}
% vertex
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colqcd,
l=\strut\colqcd$\alpha_\mathrm{s}$,l.d=6,l.a=0}{v2}
% labels
\fmfv{l.a=150,l.d=4,l=$g$}{i1}
\fmfv{l.a=-150,l.d=4,l=$g$}{i2}
\fmfv{l.a=25,l=$\tau^-$}{o1}
\fmfv{l.a=-20,l=$\overline{\mathrm{b}}$}{o2}
\fmfv{l.a=25,l=$\tau^+$}{o3}
\fmfv{l.a=-20,l=\vspace{-2pt}b}{o4}
\end{fmfgraph*}
\end{fmfpicture}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%% NONRESONANT DILEPTON PRODUCTION %%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% NONRESONANT DILEPTON PRODUCTION - t-channel
\begin{fmfpicture}{-6,10}{3,10}{LQ_tchan} % padding (LTRB)
\begin{fmfgraph*}(110,60) % dimensions (WH)
% external vertices
\fmfleft{i2,i1}
\fmfright{o2,o1}
% main: qq -> ll
\fmf{fermion}{i1,v1,o1}
\fmf{fermion}{o2,v2,i2}
\fmf{dashes,t=0.7,l.s=right,l.d=4,label=LQ}{v1,v2} % t-channel
% vertices
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx$\lambda$,l.d=6,l.a=90}{v1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx$\lambda$,l.d=6,l.a=-90}{v2}
% labels
\fmfv{l.a=160,l=$q$}{i1}
\fmfv{l.a=20,l=$\ell^-$}{o1}
\fmfv{l.a=-170,l=$\overline{q}$}{i2}
\fmfv{l.a=-10,l=$\ell^+$}{o2}
\end{fmfgraph*}
\end{fmfpicture}
% NONRESONANT DITAU PRODUCTION - t-channel
\begin{fmfpicture}{-6,10}{4,10}{LQ_tchan_bbtautau} % padding (LTRB)
\begin{fmfgraph*}(110,60) % dimensions (WH)
% external vertices
\fmfleft{i2,i1}
\fmfright{o2,o1}
% main: qq -> ll
\fmf{fermion}{i1,v1,o1}
\fmf{fermion}{o2,v2,i2}
\fmf{dashes,t=0.7,l.s=right,l.d=4,label=LQ}{v1,v2} % t-channel
% vertices
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx$\lambda$,l.d=6,l.a=90}{v1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx$\lambda$,l.d=6,l.a=-90}{v2}
% labels
\fmfv{l.a=160,l=b}{i1}
\fmfv{l.a=20,l=$\tau^-$}{o1}
\fmfv{l.a=-170,l=$\overline{\mathrm{b}}$}{i2}
\fmfv{l.a=-10,l=$\tau^+$}{o2}
\end{fmfgraph*}
\end{fmfpicture}
% NONRESONANT DITAU PRODUCTION - t-channel, gluon splitting
\begin{fmfpicture}{-6,12}{15,14}{LQ_tchan_bbtautau_gsplit} % padding (LTRB)
\begin{fmfgraph*}(110,80) % dimensions (WH)
% external vertices
\fmfleft{i2,i1}
\fmfright{o3,o2,o1}
% incoming
\fmf{fermion,t=1.7}{i1,v1}
\fmf{gluon,t=1.7}{i2,v2}
% t-channel
\fmf{dashes,l.s=left,l.d=4,label=LQ}{v,v1} % t-channel
\fmf{fermion}{v,v2} % t-channel
% outgoing
\fmf{fermion}{v1,o1}
\fmf{fermion}{v2,o3}
\fmf{fermion}{o2,v}
% vertices
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx$\lambda$,l.d=6,l.a=90}{v1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx\strut$\lambda$,l.d=4,l.a=-65}{v}
% labels
\fmfv{l.d=6,l.a=158,l=q}{i1}
\fmfv{l.d=6,l.a=-152,l=$g$}{i2}
\fmfv{l.d=6,l.a=22,l=$\tau^-$}{o1}
\fmfv{l.d=6,l.a=0,l=$\tau^+$}{o2}
\fmfv{l.d=6,l.a=-20,l=b}{o3}
\end{fmfgraph*}
\end{fmfpicture}
% NONRESONANT DITAU PRODUCTION - t-channel, gluon splitting (straight)
\begin{fmfpicture}{6,18}{16,12}{LQ_tchan_bbtautau_gsplit_straight} % padding (LTRB)
\begin{fmfgraph*}(100,75) % dimensions (WH)
% external vertices
\fmfstraight
\fmfleft{i2,i1}
\fmfright{o3,o2,o1}
% main
\fmf{fermion}{i1,v1}
\fmf{fermion}{v1,o1}
\fmf{gluon}{i2,v2}
\fmf{fermion}{v2,o3}
\fmffreeze
\fmf{fermion}{v,v2} % t-channel
\fmf{dashes,l.s=left,l.d=5,label=LQ}{v,v1} % t-channel
\fmf{fermion,t=0}{o2,v} % tau out
% vertices
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx$\lambda$,l.d=6,l.a=90}{v1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx\strut$\lambda$,l.d=6,l.a=-160}{v}
% labels
\fmfv{l.d=6,l.a=170,l=q}{i1}
\fmfv{l.d=6,l.a=-170,l=$g$}{i2}
\fmfv{l.d=6,l.a=10,l=$\tau^-$}{o1}
\fmfv{l.d=6,l.a=0,l=\strut$\tau^+$}{o2}
\fmfv{l.d=6,l.a=-10,l=b}{o3}
\end{fmfgraph*}
\end{fmfpicture}
% NONRESONANT DITAU PRODUCTION - t-channel, double gluon splitting
\begin{fmfpicture}{3,9}{13,9}{LQ_tchan_bbtautau_gsplit2} % padding (LTRB)
\begin{fmfgraph*}(115,135) % dimensions (WH)
% external vertices
\fmfleft{d,i2,i1,d}
\fmfright{b2,o2,o1,b1}
\fmfshift{8 down}{b1}
\fmfshift{8 up}{b2}
% gluon splitting
\fmf{gluon}{g1,i1}
\fmf{gluon}{i2,g2}
\fmf{phantom,t=0.62}{g1,o1,o2,g2} % pull gluons straight right
\fmffreeze
% main: qq -> ll
\fmf{fermion}{g1,v1,o1}
\fmf{fermion}{o2,v2,g2}
\fmf{fermion}{b1,g1}
\fmf{fermion}{g2,b2}
\fmf{dashes,t=0.6,l.s=right,label=LQ}{v1,v2} % t-channel
% vertices
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx$\lambda$,l.d=6,l.a=90}{v1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx$\lambda$,l.d=6,l.a=-90}{v2}
% labels
\fmfv{l.a=160,l=$g$}{i1}
\fmfv{l.a=-170,l=$g$}{i2}
\fmfv{l.a=20,l=$\tau^-$}{o1}
\fmfv{l.a=-10,l=$\tau^+$}{o2}
\fmfv{l.a=25,l.d=4,l=\vspace{-2pt}$\overline{\mathrm{b}}$}{b1}
\fmfv{l.a=-25,l.d=4,l=b}{b2}
\end{fmfgraph*}
\end{fmfpicture}
% NONRESONANT DITAU PRODUCTION - t-channel, double gluon splitting (straight)
\begin{fmfpicture}{1,4}{15,4}{LQ_tchan_bbtautau_gsplit2_straight} % padding (LTRB)
\begin{fmfgraph*}(120,125) % dimensions (WH)
% external vertices
\fmfleft{d,i2,m2,m1,i1,d} % add dummies 'd' for spacing
\fmfright{b2,p2,o2,o1,p1,b1} % add dummies 'd' for spacing
\fmfshift{3 down}{i1,p1}
\fmfshift{3 up}{i2,p2}
\fmfshift{7 down}{b1,o2}
\fmfshift{7 up}{b2,o1}
% incoming
\fmf{gluon}{v1,i1}
\fmf{gluon}{i2,v2}
\fmf{phantom,t=0.6}{v1,p1,p2,v2} % pull gluons straight right
\fmffreeze
%%%% outgoing tau leptons
%%%\fmf{fermion}{lq1,o1} % tau out
%%%\fmf{fermion}{o2,lq2} % tau out
%%%\fmf{phantom,t=0.5}{lq1,m1,m2,lq2} % pull taus straight left
%%%\fmffreeze
%%% outgoing b quarks from gluon splitting
\fmf{fermion}{b1,v1}
\fmf{fermion}{v2,b2}
% t-channel
\fmf{fermion}{v1,lq1} % t-channel
\fmf{dashes,t=0.8,l.s=right,l.d=5,label=LQ}{lq1,lq2} % t-channel
\fmf{fermion}{lq2,v2} % t-channel
% outgoing tau leptons
\fmf{fermion,t=0.9}{lq1,o1} % tau out
\fmf{fermion,t=0.9}{o2,lq2} % tau out
% vertices
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx$\lambda$,l.d=6,l.a=90}{lq1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx$\lambda$,l.d=6,l.a=-90}{lq2}
% labels
\fmfv{l.d=6,l.a=170,l=$g$}{i1}
\fmfv{l.d=6,l.a=-170,l=$g$}{i2}
\fmfv{l.d=6,l.a=10,l=$\tau^-$}{o1}
\fmfv{l.d=6,l.a=0,l=\strut$\tau^+$}{o2}
\fmfv{l.d=6,l.a=20,l=$\overline{\mathrm{b}}$}{b1}
\fmfv{l.d=6,l.a=-20,l=b}{b2}
\end{fmfgraph*}
\end{fmfpicture}
% NONRESONANT DITAU PRODUCTION - t-channel, double gluon splitting (square)
\begin{fmfpicture}{6,12}{16,12}{LQ_tchan_bbtautau_gsplit2_square} % padding (LTRB)
\begin{fmfgraph*}(100,90) % dimensions (WH)
% external vertices
\fmfstraight
\fmfleft{i2,i1}
\fmfright{b2,o2,o1,b1}
% incoming
\fmf{gluon}{v1,i1}
\fmf{gluon}{i2,v2}
% outgoing b quarks from gluon splitting
\fmf{fermion}{b1,v1}
\fmf{fermion}{v2,b2}
\fmffreeze
% t-channel
\fmf{fermion}{v1,lq1} % t-channel
\fmf{dashes,l.s=right,l.d=5,label=LQ}{lq1,lq2} % t-channel
\fmf{fermion}{lq2,v2} % t-channel
\fmffreeze
% outgoing tau leptons
\fmf{fermion}{lq1,o1} % tau out
\fmf{fermion}{o2,lq2} % tau out
% vertices
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx$\lambda$,l.d=5,l.a=140}{lq1}
\fmfv{d.sh=circle,d.f=full,d.si=4,f=colvtx,
l=\colvtx\vspace{-2pt}$\lambda$,l.d=5,l.a=-160}{lq2}
% labels
\fmfv{l.d=6,l.a=170,l=$g$}{i1}
\fmfv{l.d=6,l.a=-170,l=$g$}{i2}
\fmfv{l.d=6,l.a=10,l=$\tau^-$}{o1}
\fmfv{l.d=6,l.a=0,l=\strut$\tau^+$}{o2}
\fmfv{l.d=6,l.a=10,l=$\overline{\mathrm{b}}$}{b1}
\fmfv{l.d=6,l.a=-10,l=b}{b2}
\end{fmfgraph*}
\end{fmfpicture}
\end{document}Click to download: LQ.tex (LQ_colored.tex) • LQ.pdf (LQ_colored.pdf)
Open in Overleaf: LQ.tex