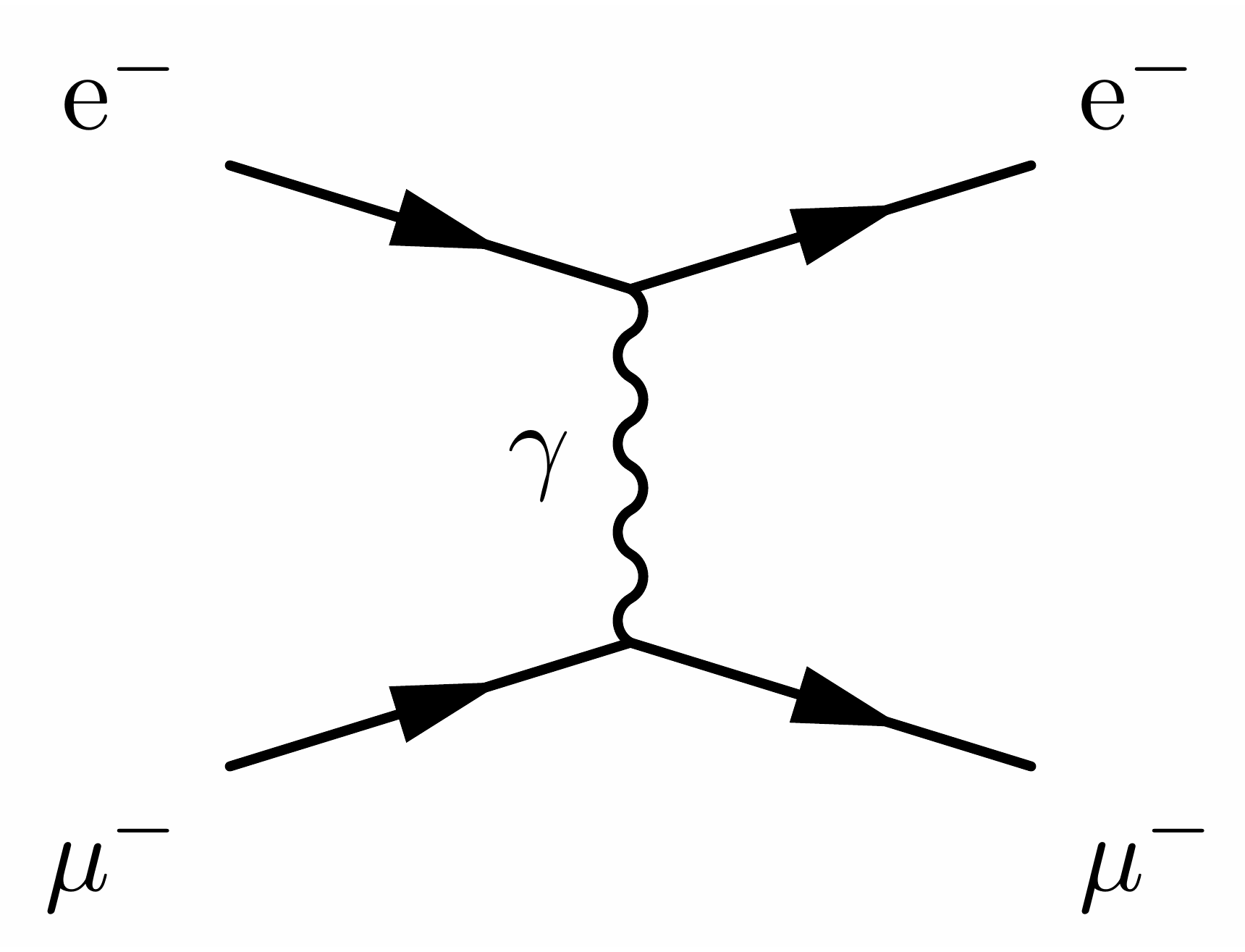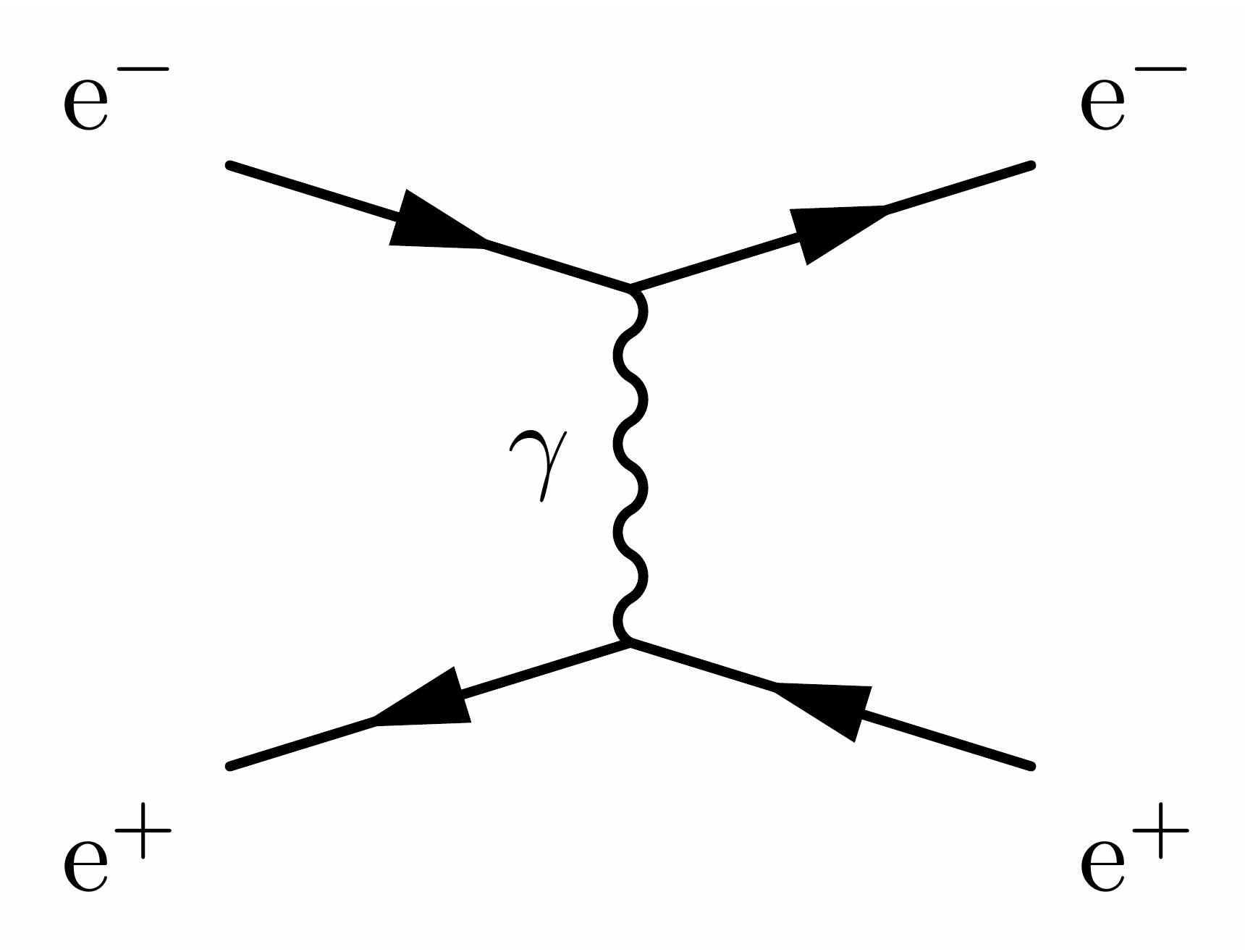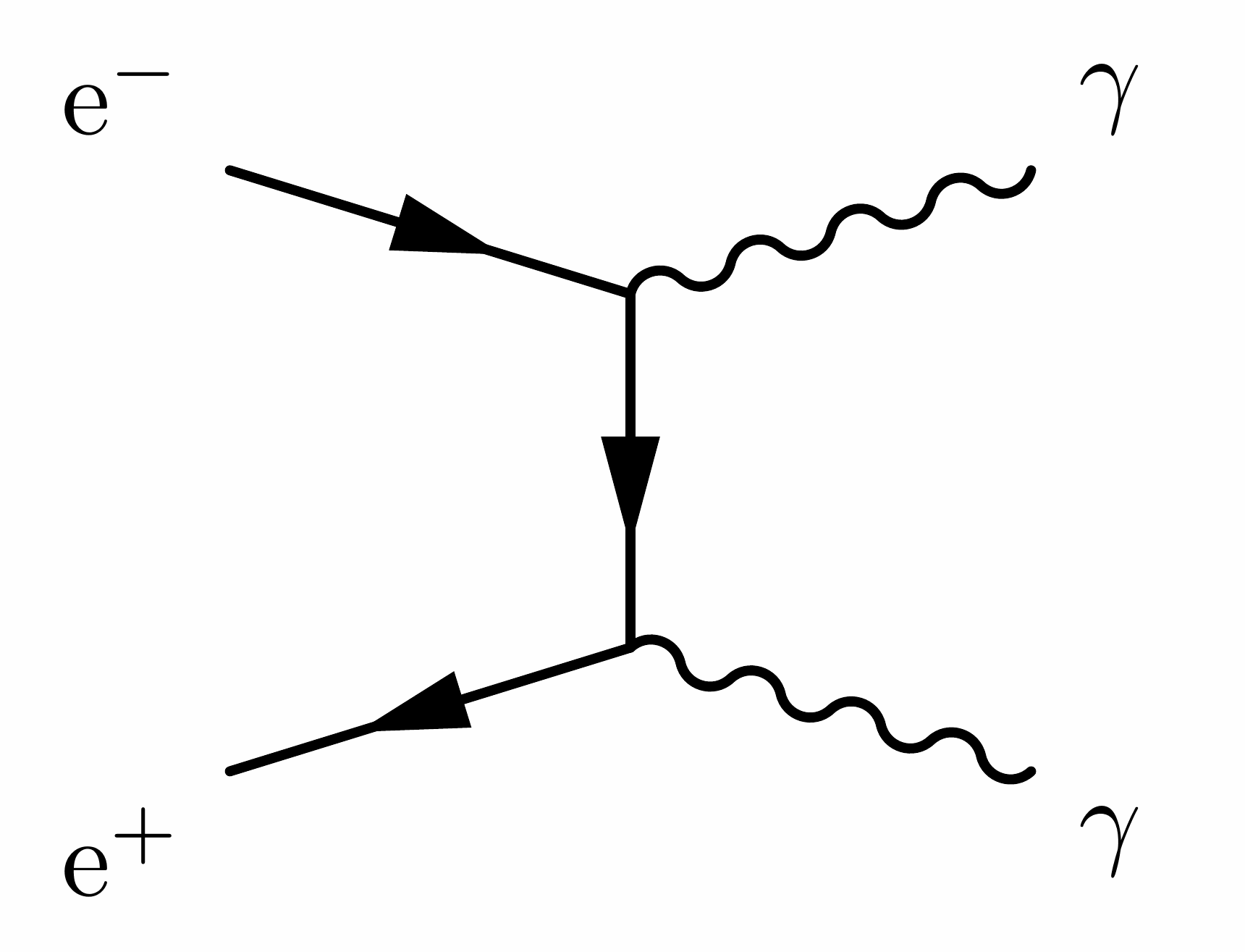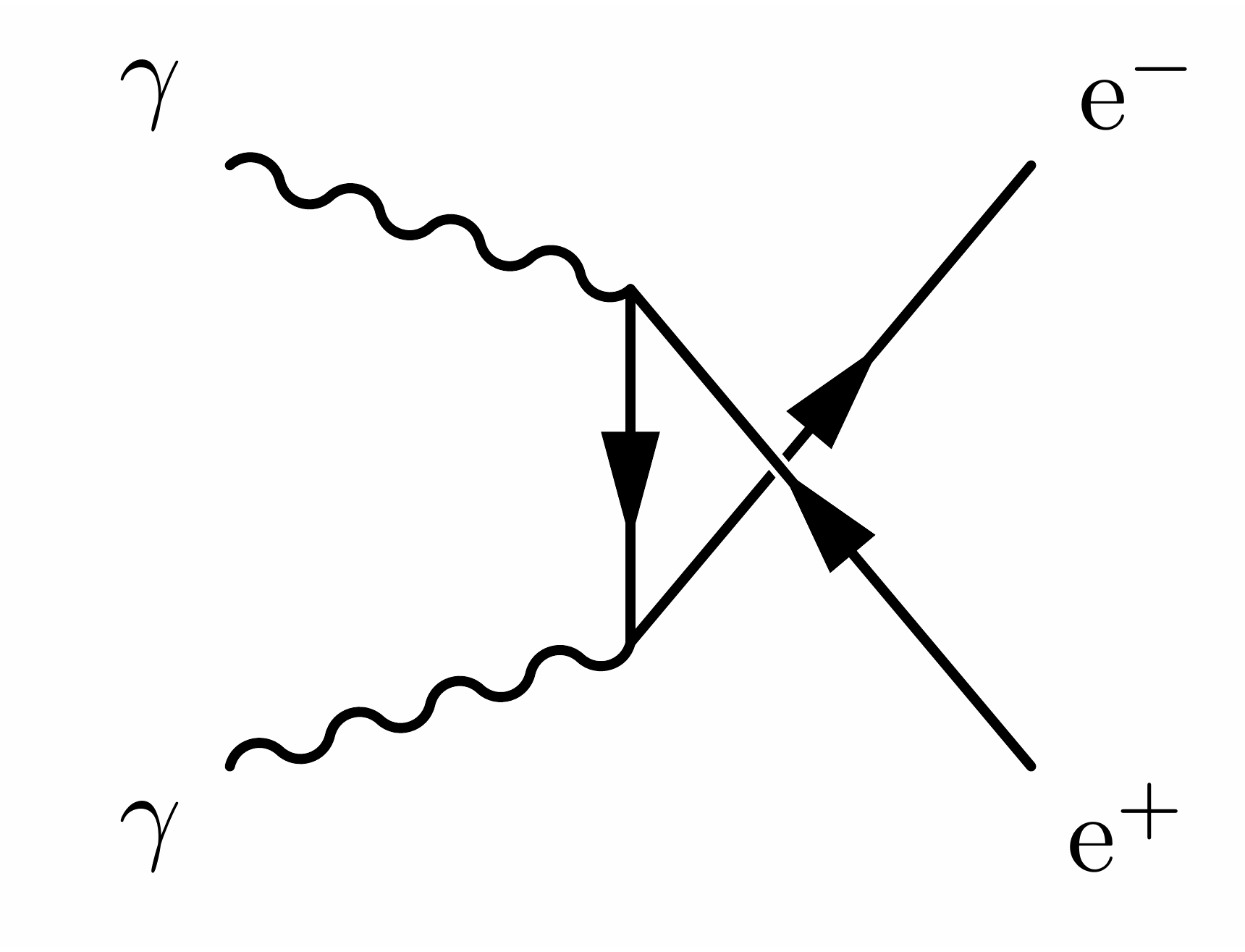
Below are some code examples of Feynman diagrams showing hard processes in proton-proton collisions.
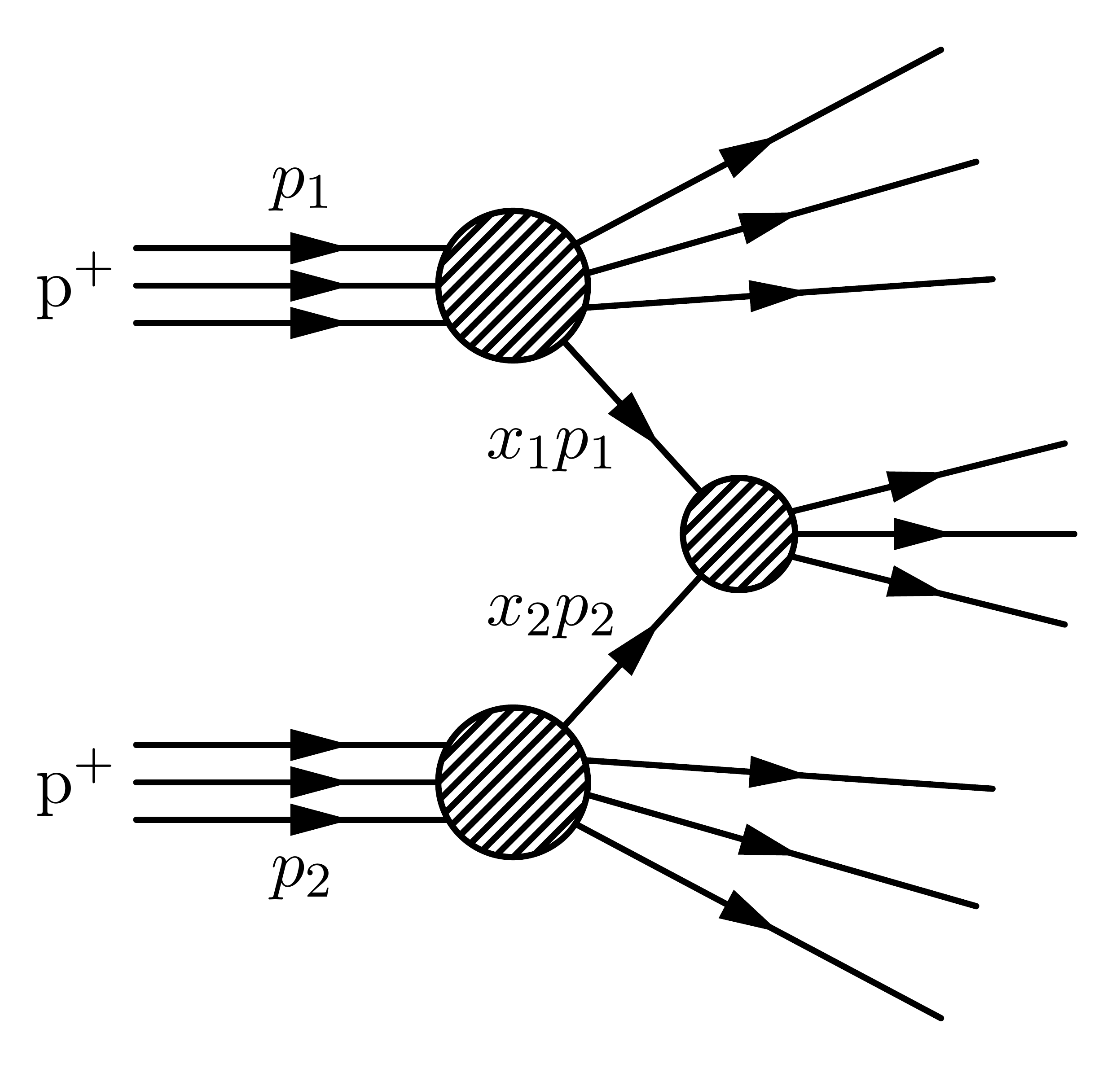
Click on a diagram to jump to the code & download links below:Inelastic hard process:
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(-2,44)(0,44){ % padding (L,T)(R,B)
\begin{fmfgraph*}(160,80) % dimensions (WH)
% line style
\fmfset{arrow_len}{10} % arrow length
% external vertices
\fmfleft{ip2,ip1}
\fmfright{op2,o,op1}
% skeleton
\fmf{phantom}{ip1,vp1,op1} % predefine path for \fmfi
\fmf{phantom}{ip2,vp2,op2} % predefine path for \fmfi
\fmf{phantom,t=0.3}{vp1,ip1,ip2,vp2} % pull proton blobs to left
\fmffreeze
% incoming proton 1
\fmfv{l=$\mathrm{p}^+$,l.a=180,l.d=8}{ip1}
\fmf{phantom}{ip1,vp1}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5, 6)}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5, 0)}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5,-6)}
%incoming proton 2
\fmfv{l=$\mathrm{p}^+$,l.a=180,l.d=8}{ip2}
\fmf{phantom}{ip2,vp2}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5, 6)}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5, 0)}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5,-6)}
% fragmented proton X_1
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),28) shifted (5, 4)}
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),16) shifted (5, 0)}
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1), 4) shifted (5,-4)}
% fragmented proton X_2
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2), -4) shifted (5, 4)}
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-16) shifted (5, 0)}
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-28) shifted (5,-4)}
% proton blobs (draw after \fmfi!)
\fmfblob{24}{vp1}
\fmfblob{24}{vp2}
\fmf{phantom,l.s=left,l.d=12,label=$p_1$}{ip1,vp1}
\fmf{phantom,l.s=right,l.d=12,label=$p_2$}{ip2,vp2}
% partons incoming from proton
\fmf{fermion,l.d=3,l.s=right,label=$x_1p_1$}{vp1,v}
\fmf{fermion,l.d=3,l.s=left,label=$x_2p_2$}{vp2,v}
% hard interaction
\fmf{phantom,t=1.4}{v,o} % predefine path path \fmfi
\fmffreeze
\fmfi{fermion}{vpath (__v,__o) rotatedaround(vloc(__v), 14) shifted (2, 2)}
\fmfi{fermion}{vpath (__v,__o) rotatedaround(vloc(__v), 0) shifted (2, 0)}
\fmfi{fermion}{vpath (__v,__o) rotatedaround(vloc(__v),-14) shifted (2,-2)}
\fmfblob{18}{v}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
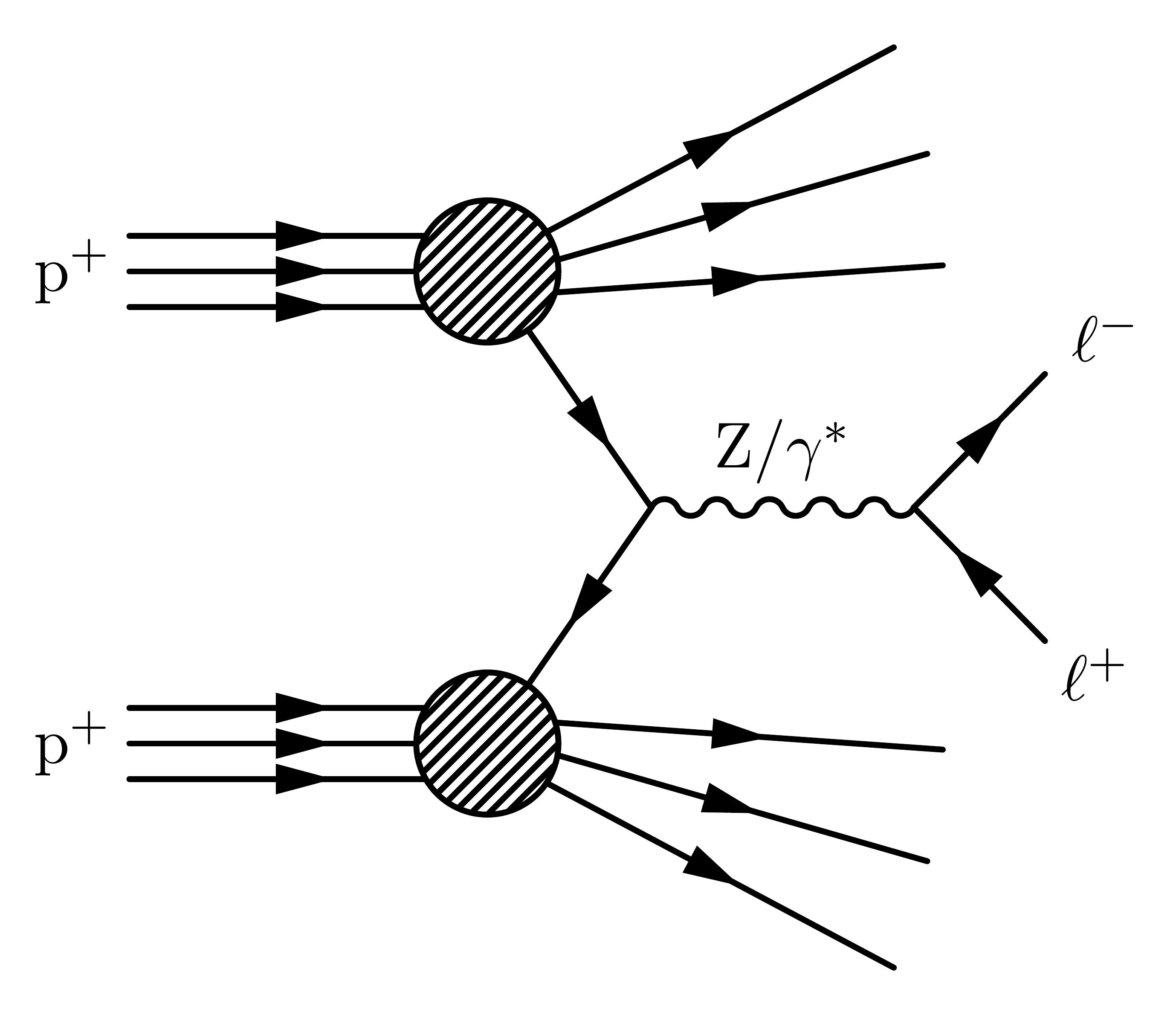
Drell–Yan production of two same-flavored fermions:
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(-2,44)(19,44){ % padding (L,T)(R,B)
\begin{fmfgraph*}(160,80) % dimensions (WH)
% line style
\fmfset{arrow_len}{10} % arrow length
\fmfset{wiggly_len}{12} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfleft{ip2,ip1}
\fmfright{op2,f1,f2,op1} % add dummies 'd' for spacing
\fmfshift{8 right}{f1,f2}
\fmfshift{8 down}{f1}
\fmfshift{8 up}{f2}
% skeleton
\fmf{phantom}{ip1,vp1,op1} % predefine path for \fmfi
\fmf{phantom}{ip2,vp2,op2} % predefine path for \fmfi
\fmf{phantom,t=0.3}{vp1,ip1,ip2,vp2} % pull proton blobs to left
\fmffreeze
% incoming proton 1
\fmfv{l=$\mathrm{p}^+$,l.a=180,l.d=8}{ip1}
\fmf{phantom}{ip1,vp1}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5, 6)}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5, 0)}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5,-6)}
%incoming proton 2
\fmfv{l=$\mathrm{p}^+$,l.a=180,l.d=8}{ip2}
\fmf{phantom}{ip2,vp2}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5, 6)}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5, 0)}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5,-6)}
% fragmented proton X_1
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),28) shifted (5, 4)}
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),16) shifted (5, 0)}
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1), 4) shifted (5,-4)}
% fragmented proton X_2
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2), -4) shifted (5, 4)}
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-16) shifted (5, 0)}
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-28) shifted (5,-4)}
% proton blobs (draw after \fmfi!)
\fmfblob{24}{vp1}
\fmfblob{24}{vp2}
% partons incoming from proton
\fmf{fermion,t=1.6}{vp1,v}
\fmf{fermion,t=1.6}{v,vp2}
% hard process
\fmf{boson,t=2,l.d=4,l.s=left,label=$\mathrm{Z}/\gamma^*$}{v,vf}
\fmf{fermion,t=2}{f1,vf,f2}
% labels
\fmfv{l.a=-25,l.d=3,l=$\ell^+$}{f1}
\fmfv{l.a=25,l.d=5,l=$\ell^-$}{f2}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
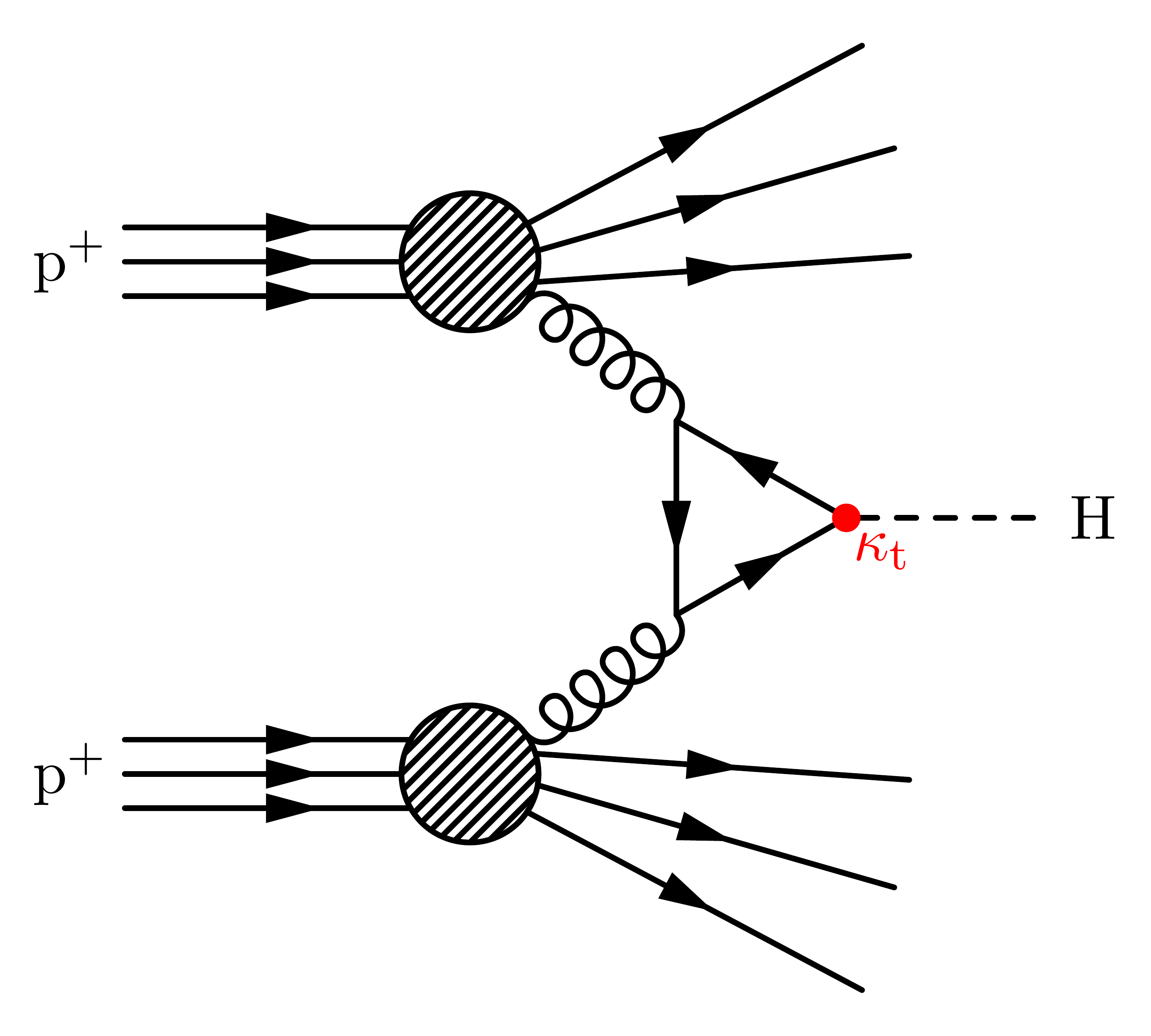
Higgs boson production via gluon-fusion:
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colkappaf}{rgb}{1,0,0} % kappa_f (red)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(-2,44)(22,44){ % padding (L,T)(R,B)
\begin{fmfgraph*}(160,90) % dimensions (WH)
% line style
\fmfset{arrow_len}{10} % arrow length
\fmfset{dash_len}{8} % dashes length
\fmfset{curly_len}{7}
% external vertices
\fmfleft{ip2,ip1}
\fmfright{op2,o,op1}
\fmfshift{14 right}{o}
% skeleton
\fmf{phantom}{ip1,vp1,op1} % predefine path for \fmfi
\fmf{phantom}{ip2,vp2,op2} % predefine path for \fmfi
\fmf{phantom,t=0.3}{vp1,ip1,ip2,vp2} % pull proton blobs to left
\fmffreeze
% incoming proton 1
\fmfv{l=$\mathrm{p}^+$,l.a=180,l.d=8}{ip1}
\fmf{phantom}{ip1,vp1}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5, 6)}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5, 0)}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5,-6)}
%incoming proton 2
\fmfv{l=$\mathrm{p}^+$,l.a=180,l.d=8}{ip2}
\fmf{phantom}{ip2,vp2}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5, 6)}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5, 0)}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5,-6)}
% fragmented proton X_1
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),28) shifted (5, 4)}
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),16) shifted (5, 0)}
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1), 4) shifted (5,-4)}
% fragmented proton X_2
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2), -4) shifted (5, 4)}
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-16) shifted (5, 0)}
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-28) shifted (5,-4)}
% proton blobs (draw after \fmfi!)
\fmfblob{24}{vp1}
\fmfblob{24}{vp2}
% partons incoming from proton
\fmf{gluon,t=1.4}{v1,vp1}
\fmf{gluon,t=1.4}{vp2,v2}
% hard process
\fmf{fermion,t=0.3}{v1,v2}
\fmf{fermion,t=1.7}{v2,vh,v1}
\fmf{dashes,t=2.8}{vh,o}
% vertices
\fmfv{decor.shape=circle,decor.filled=full,decor.size=4,f=(1,,0,,0),
l.d=3,l.a=-65,l=\color{colkappaf}$\kappa_\mathrm{t}$}{vh}
% labels
\fmfv{l.a=0,l.d=3,l=H}{o}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
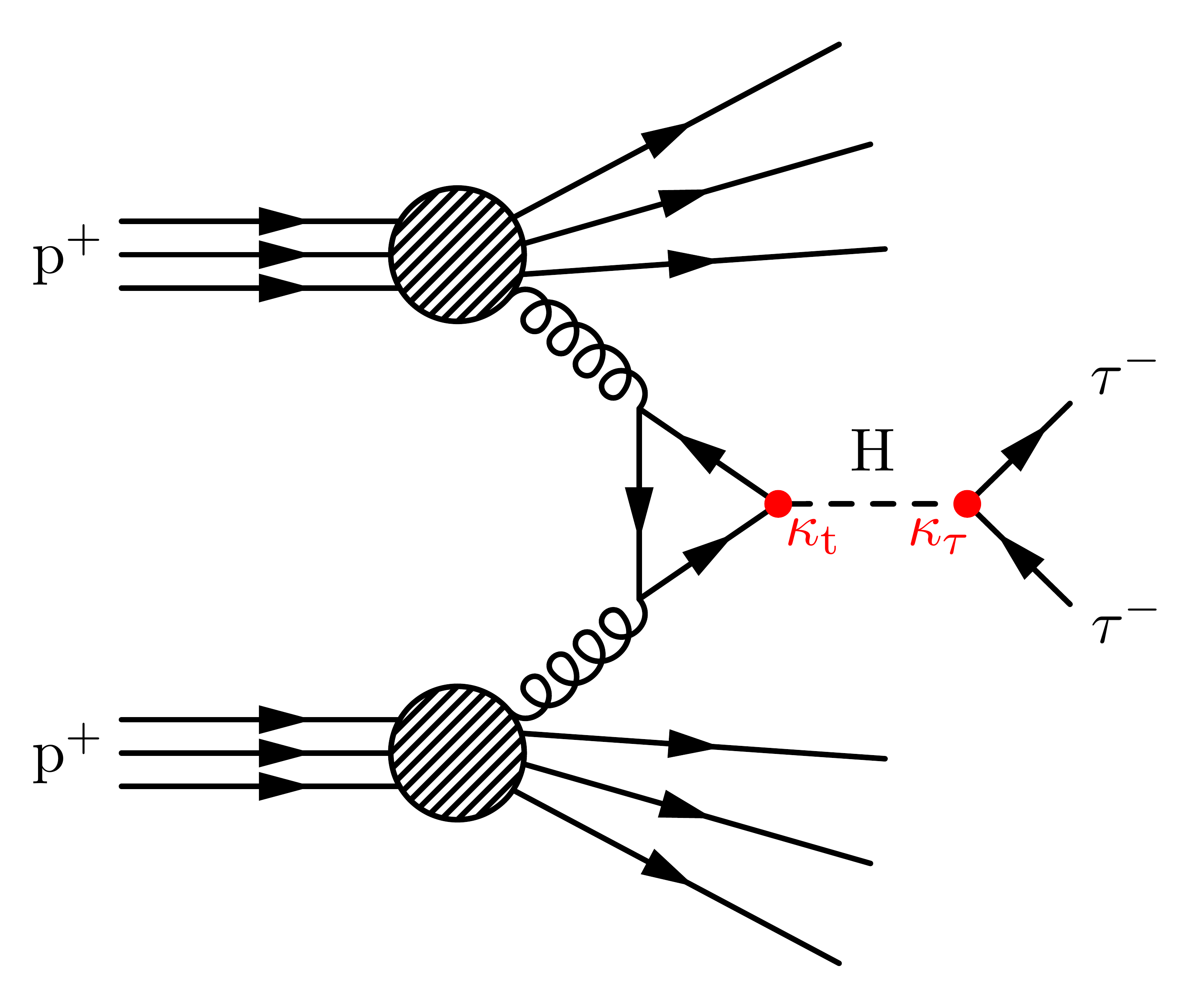
With Higgs boson decay:
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colkappaf}{rgb}{1,0,0} % kappa_f (red)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(-2,44)(36,44){ % padding (L,T)(R,B)
\begin{fmfgraph*}(160,90) % dimensions (WH)
% line style
\fmfset{arrow_len}{10} % arrow length
\fmfset{dash_len}{8} % dashes length
\fmfset{curly_len}{7}
% external vertices
\fmfleft{ip2,ip1}
\fmfright{op2,o2,o1,op1}
\fmfshift{24 right}{o1,o2}
\fmfshift{2 up}{o1}
\fmfshift{2 down}{o2}
% skeleton
\fmf{phantom}{ip1,vp1,op1} % predefine path for \fmfi
\fmf{phantom}{ip2,vp2,op2} % predefine path for \fmfi
\fmf{phantom,t=0.3}{vp1,ip1,ip2,vp2} % pull proton blobs to left
\fmffreeze
% incoming proton 1
\fmfv{l=$\mathrm{p}^+$,l.a=180,l.d=8}{ip1}
\fmf{phantom}{ip1,vp1}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5, 6)}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5, 0)}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5,-6)}
%incoming proton 2
\fmfv{l=$\mathrm{p}^+$,l.a=180,l.d=8}{ip2}
\fmf{phantom}{ip2,vp2}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5, 6)}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5, 0)}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5,-6)}
% fragmented proton X_1
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),28) shifted (5, 4)}
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),16) shifted (5, 0)}
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1), 4) shifted (5,-4)}
% fragmented proton X_2
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2), -4) shifted (5, 4)}
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-16) shifted (5, 0)}
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-28) shifted (5,-4)}
% proton blobs (draw after \fmfi!)
\fmfblob{24}{vp1}
\fmfblob{24}{vp2}
% incoming parton
\fmf{gluon,t=1.3}{v1,vp1}
\fmf{gluon,t=1.3}{vp2,v2}
% hard process
\fmf{fermion,t=0.2}{v1,v2}
\fmf{fermion,t=1.7}{v2,vh1,v1}
\fmf{dashes,t=2.5,l.s=left,label=H}{vh1,vh2}
% decay
\fmf{fermion,t=2.3}{o2,vh2,o1}
% vertices
\fmfv{decor.shape=circle,decor.filled=full,decor.size=4,f=(1,,0,,0),
l.d=3,l.a=-65,l=\color{colkappaf}$\kappa_\mathrm{t}$}{vh1}
\fmfv{decor.shape=circle,decor.filled=full,decor.size=4,f=(1,,0,,0),
l.d=3,l.a=-115,l=\color{colkappaf}$\kappa_\tau$\hspace{-2pt}}{vh2}
% labels
\fmfv{l.a=25,l.d=4,l=$\tau^-$}{o1}
\fmfv{l.a=-20,l.d=4,l=\vspace{-2mm}\strut$\tau^-$}{o2}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
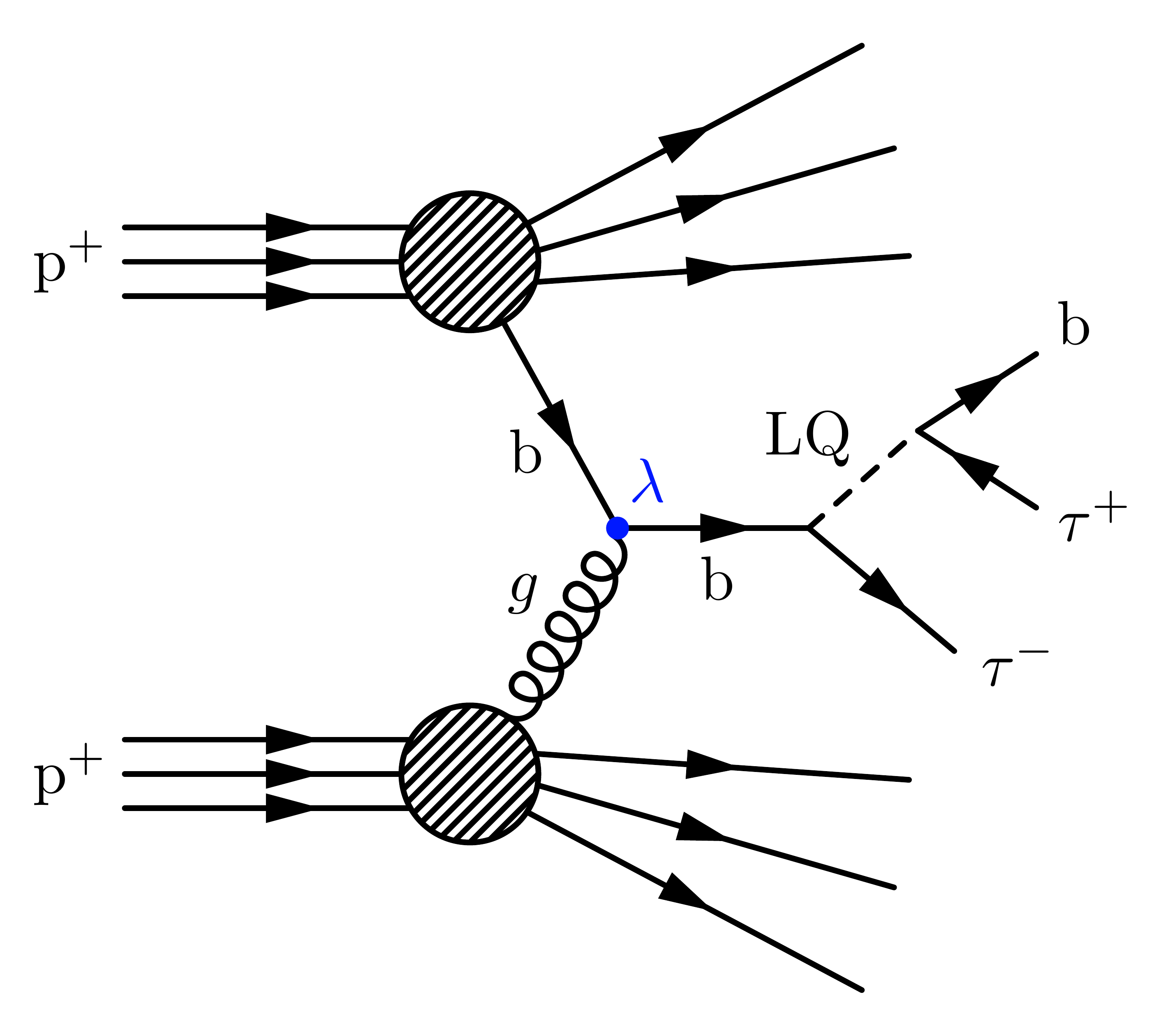
Single LQ production, where one proton stays intact (for more LQ diagrams, see the LQ category):
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colvtx}{rgb}{0,.1,1} % LQ vertex (blue)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(-2,44)(25,44){ % padding (L,T)(R,B)
\begin{fmfgraph*}(160,90) % dimensions (WH)
% line style
\fmfset{arrow_len}{10} % arrow length
\fmfset{dash_len}{8} % dashes length
\fmfset{curly_len}{7}
% external vertices
\fmfleft{ip2,ip1}
\fmfright{op2,o3,o2,o1,op1}
\fmfforce{(1.07w,.82h)}{o1} % exact placement
\fmfforce{(1.07w,.52h)}{o2} % exact placement
\fmfforce{(0.98w,.24h)}{o3} % exact placement
% internal vertices (exact placement)
\fmfforce{(.61w,.48h)}{v1} % exact placement
\fmfforce{(.82w,.48h)}{v2} % exact placement
\fmfforce{(.94w,.67h)}{lq} % exact placement
% skeleton
\fmf{phantom}{ip1,vp1,op1} % predefine path for \fmfi
\fmf{phantom}{ip2,vp2,op2} % predefine path for \fmfi
\fmf{phantom,t=0.3}{vp1,ip1,ip2,vp2} % pull proton blobs to left
\fmffreeze
% incoming proton 1
\fmfv{l=$\mathrm{p}^+$,l.a=180,l.d=8}{ip1}
\fmf{phantom}{ip1,vp1}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5, 6)}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5, 0)}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5,-6)}
%incoming proton 2
\fmfv{l=$\mathrm{p}^+$,l.a=180,l.d=8}{ip2}
\fmf{phantom}{ip2,vp2}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5, 6)}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5, 0)}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5,-6)}
% fragmented proton X_1
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),28) shifted (5, 4)}
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),16) shifted (5, 0)}
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1), 4) shifted (5,-4)}
% fragmented proton X_2
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2), -4) shifted (5, 4)}
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-16) shifted (5, 0)}
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-28) shifted (5,-4)}
% proton blobs (draw after \fmfi!)
\fmfblob{24}{vp1}
\fmfblob{24}{vp2}
% parton & photon incoming from proton
\fmf{fermion,l.d=3,l.s=right,label=b}{vp1,v1}
\fmf{gluon,l.d=4,l.s=left,label=$g$}{vp2,v1}
\fmf{fermion,l.d=5,l.s=right,label=b}{v1,v2} % s-channel
% LQ -> btau
\fmf{dashes,t=2.9,l.d=3,l.s=left,label=LQ}{v2,lq}
\fmf{fermion,t=1.7}{o2,lq,o1}
\fmf{fermion,t=0.3}{v2,o3}
% vertex
\fmfv{d.shape=circle,d.fill=full,d.si=3,f=(0,,.1,,1),
l=\color{colvtx}$\lambda$,l.d=5,l.a=66}{v1}
% labels
\fmfv{l.a=25,l.d=4,l=b}{o1}
\fmfv{l.a=20,l.d=4,l=\vspace{-2mm}$\tau^+$}{o2}
\fmfv{l.a=-20,l.d=5,l=$\tau^-$}{o3}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
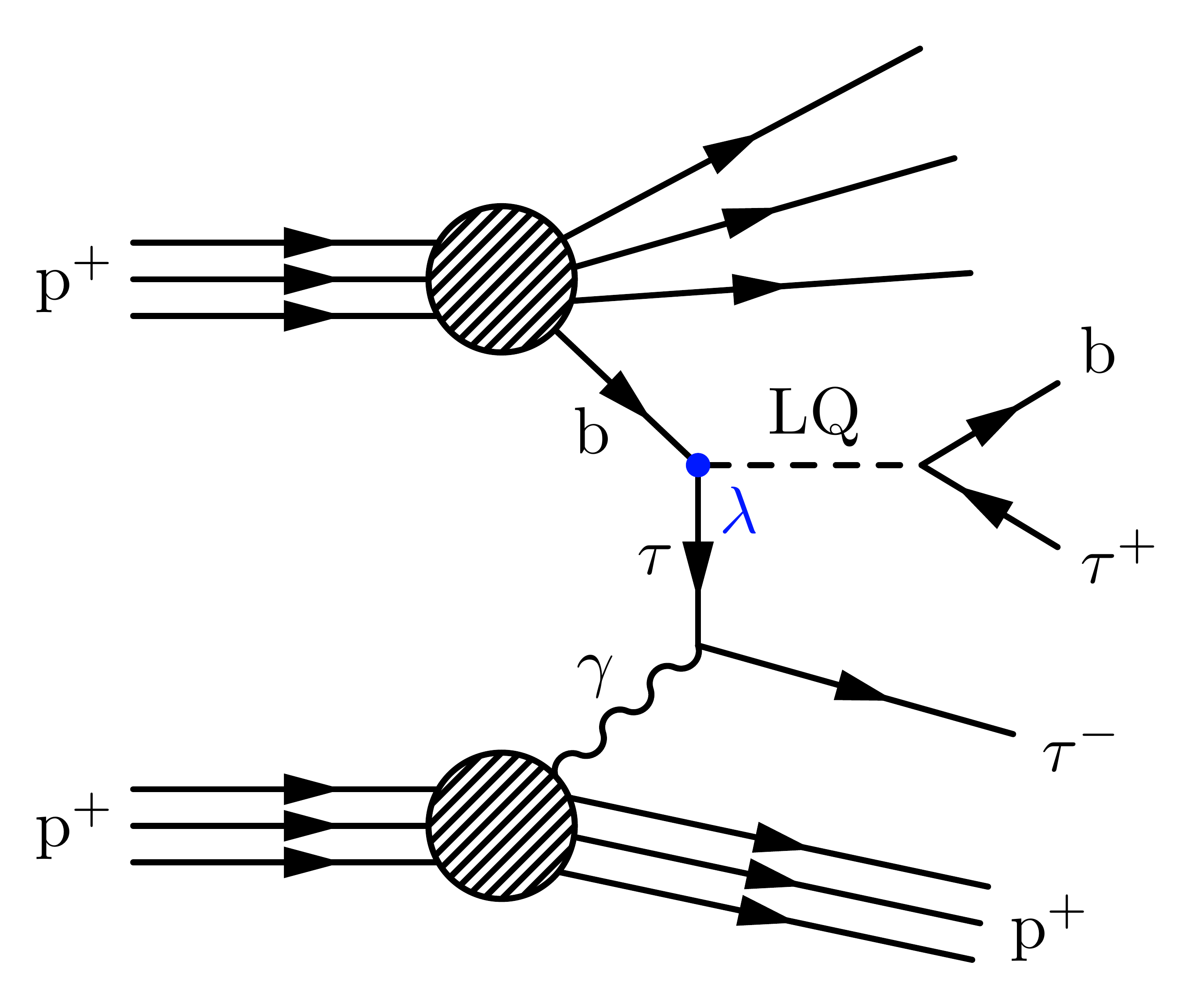
Photon-induced single LQ production, where one proton stays intact (for more LQ diagrams, see the LQ category):
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colvtx}{rgb}{0,.1,1} % LQ vertex (blue)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(-2,44)(16,28){ % padding (L,T)(R,B)
\begin{fmfgraph*}(160,90) % dimensions (WH)
% line style
\fmfset{arrow_len}{10} % arrow length
\fmfset{dash_len}{8} % dashes length
% external vertices
\fmfleft{ip2,ip1}
\fmfright{op2,o3,o2,o1,op1}
\fmfshift{6 down}{o3}
\fmfforce{(1.02w,.81h)}{o1} % exact placement
\fmfforce{(1.02w,.51h)}{o2} % exact placement
% internal vertices (exact placement)
\fmfforce{(.65w,.66h)}{v1} % exact placement
\fmfforce{(.65w,.33h)}{v2} % exact placement
\fmfforce{(.88w,.66h)}{lq} % exact placement
% skeleton
\fmf{phantom}{ip1,vp1,op1} % predefine path for \fmfi
\fmf{phantom}{ip2,vp2,op2} % predefine path for \fmfi
\fmf{phantom,t=0.3}{vp1,ip1,ip2,vp2} % pull proton blobs to left
\fmffreeze
% incoming proton 1
\fmfv{l=$\mathrm{p}^+$,l.a=180,l.d=8}{ip1}
\fmf{phantom}{ip1,vp1}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5, 6)}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5, 0)}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5,-6)}
%incoming proton 2
\fmfv{l=$\mathrm{p}^+$,l.a=180,l.d=8}{ip2}
\fmf{phantom}{ip2,vp2}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5, 6)}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5, 0)}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5,-6)}
% fragmented proton X
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),28) shifted (5, 4)}
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),16) shifted (5, 0)}
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1), 4) shifted (5,-4)}
% outgoing intact proton
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-12) shifted (9.3, 5)}
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-12) shifted (8.0,-1)}
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-12) shifted (6.7,-7)}
% blobs (draw after \fmfi!)
\fmfblob{24}{vp1}
\fmfblob{24}{vp2}
% parton & photon incoming from proton
\fmf{fermion,l.d=3,l.s=right,label=b}{vp1,v1}
\fmf{photon,l.d=3,l.s=left,label=$\gamma$}{vp2,v2}
\fmf{fermion,l.d=4,l.s=right,label=$\tau$}{v1,v2} % t-channel
% LQ -> btau
\fmf{dashes,t=2.9,l.d=3,l.s=left,label=LQ}{v1,lq}
\fmf{fermion,t=1.7}{o2,lq,o1}
\fmf{fermion,t=0.3}{v2,o3}
% vertex
\fmfv{d.shape=circle,d.fill=full,d.si=3,f=(0,,.1,,1),
l=\color{colvtx}$\lambda$,l.d=5,l.a=-45}{v1}
% labels
\fmfv{l=$\mathrm{p}^+$,l.a=-45,l.d=16}{op2}
\fmfv{l.a=25,l.d=4,l=b}{o1}
\fmfv{l.a=20,l.d=4,l=\vspace{-2mm}$\tau^+$}{o2}
\fmfv{l.a=-20,l.d=5,l=$\tau^-$}{o3}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
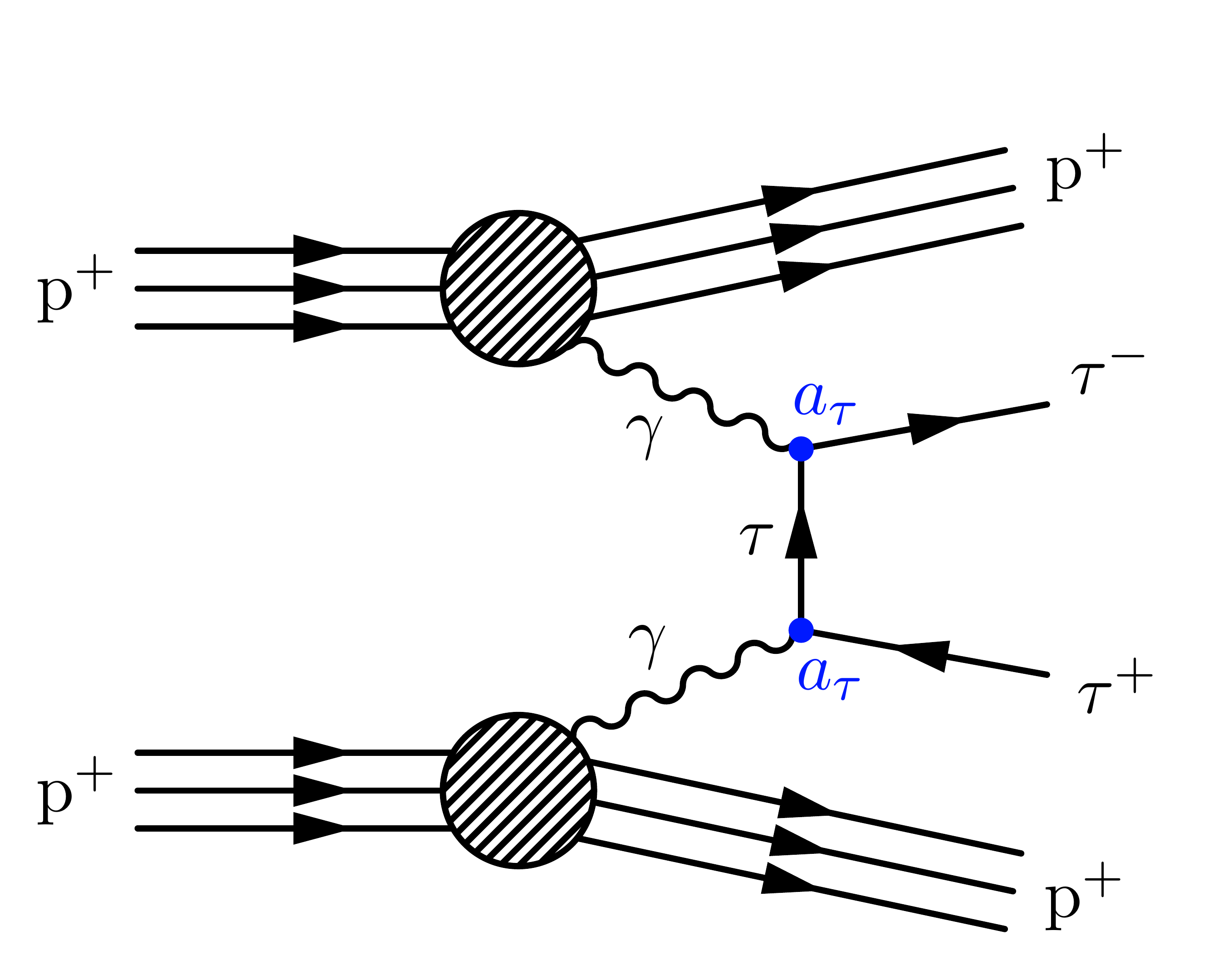
Photon-induced (also see this post or this experimental paper by CMS):
\documentclass[11pt,border=4pt]{standalone}
\usepackage{feynmp-auto}
\usepackage{xcolor}
\definecolor{colvtx}{rgb}{0,.1,1} % LQ vertex (blue)
\begin{document}
\begin{fmffile}{feyngraph}
\fmfframe(-2,44)(16,28){ % padding (L,T)(R,B)
\begin{fmfgraph*}(160,80) % dimensions (WH)
% line style
\fmfset{arrow_len}{10} % arrow length
\fmfset{wiggly_len}{11} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
% external vertices
\fmfleft{ip2,ip1}
\fmfright{op2,o2,d,o1,op1}
% skeleton
\fmf{phantom}{ip1,vp1,op1} % predefine path for \fmfi
\fmf{phantom}{ip2,vp2,op2} % predefine path for \fmfi
\fmf{phantom,t=0.3}{vp1,ip1,ip2,vp2} % pull proton blobs to left
\fmffreeze
% incoming proton 1
\fmfv{l=$\mathrm{p}^+$,l.a=180,l.d=8}{ip1}
\fmf{phantom}{ip1,vp1}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5, 6)}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5, 0)}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5,-6)}
%incoming proton 2
\fmfv{l=$\mathrm{p}^+$,l.a=180,l.d=8}{ip2}
\fmf{phantom}{ip2,vp2}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5, 6)}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5, 0)}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5,-6)}
% outgoing intact proton 1
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),12) shifted (6.7, 7)}
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),12) shifted (8.0, 1)}
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),12) shifted (9.3,-5)}
% outgoing intact proton 2
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-12) shifted (9.3, 5)}
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-12) shifted (8.0,-1)}
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-12) shifted (6.7,-7)}
% blobs (draw after \fmfi!)
\fmfblob{24}{vp1}
\fmfblob{24}{vp2}
% incoming photons from protons
\fmfforce{0.06[vloc(__vp1),vloc(__vp2)]}{q1} % exact placement
\fmfforce{0.06[vloc(__vp2),vloc(__vp1)]}{q2} % exact placement
\fmf{photon,l.d=6,l.s=right,label=$\gamma$\hspace{-4pt}}{q1,v1}
\fmf{photon,l.d=5,l.s=left,label=$\gamma$\hspace{-4pt}}{q2,v2}
\fmf{fermion,l.d=4,l.s=left,label=$\tau$}{v2,v1} % t-channel
% LQ -> btau
\fmf{fermion,t=1.15}{v1,o1}
\fmf{fermion,t=1.15}{o2,v2}
% vertex
\fmfv{d.shape=circle,d.fill=full,d.si=3,f=(0,,.1,,1),
l=\color{colvtx}\hspace{6pt}$a_\tau$,l.d=4,l.a=75}{v1}
\fmfv{d.shape=circle,d.fill=full,d.si=3,f=(0,,.1,,1),
l=\color{colvtx}\hspace{6pt}$a_\tau$,l.d=5,l.a=-70}{v2}
% labels
\fmfv{l=$\mathrm{p}^+$,l.a=50,l.d=18}{op1}
\fmfv{l=$\mathrm{p}^+$,l.a=-45,l.d=16}{op2}
\fmfv{l.a=25,l.d=4,l=$\tau^-$}{o1}
\fmfv{l.a=-20,l.d=5,l=$\tau^+$}{o2}
\end{fmfgraph*}
} % close \fmfframe
\end{fmffile}
\end{document}
Full code
The LaTeX code below collects all the diagrams above into one big file that produces a multipage PDF. Please find download links below, or edit and compile here if you like:
% !TEX program = pdflatexmk
% !TEX parameter = -shell-escape
% Author: Izaak Neutelings (September 2024)
% Instructions: To compile via command line, run the following twice
% pdflatex -shell-escape pp_hard.tex
\documentclass[11pt,border=2pt,multi=page,crop]{standalone}
\usepackage{graphicx}
\usepackage{feynmp-auto}
% DEFINE TEXT COLORS
\usepackage{xcolor}
\definecolor{colvtx}{rgb}{0,.1,1} % LQ vertex (blue)
\definecolor{colkappaf}{rgb}{1,0,0} % kappa_f (red)
% DEFINE COLOR MACROS
% The following loops over the user color names and defines
% a handy \<colname> command to set text color, as well as
% defines colors in MetaPost of the same and value for lines
\usepackage{pgffor} % for \foreach
\def\MPcolors{} % MetaPost code importing xcolor names
\foreach \colname in {colvtx,colkappaf}{ % create command & MetaPost code
\expandafter\xdef\csname\colname\endcsname{\noexpand\color{\colname}} % \newcommand\<colname>
\convertcolorspec{named}{\colname}{rgb}\tmprgb % get rgb code
\xdef\MPcolors{\MPcolors color \colname; \colname := (\tmprgb); } % add color name
}
% DEFINE fmfpicture ENVIRONMENT
\usepackage{environ} % for \NewEnviron
\NewEnviron{fmfpicture}[3]{%
\begin{page} % to create standalone page
\fmfframe(#1)(#2){ % padding (LT)(RB)
\begin{fmffile}{feynmp-#3} % auxiliary files (use unp2ue name!)
\fmfset{arrow_len}{10} % arrow length
\fmfset{dash_len}{8} % dashes length
\fmfset{wiggly_len}{11} % boson wavelength
\fmfset{wiggly_slope}{65} % boson slope of waves
\fmfcmd\MPcolors % define custom line colors in MetaPost
\BODY % main code
\end{fmffile}
}
\end{page}
}
% CUSTOM DRAW MACROS
\def\drawprotons{
% skeleton
\fmf{phantom}{ip1,vp1,op1} % predefine path for \fmfi
\fmf{phantom}{ip2,vp2,op2} % predefine path for \fmfi
\fmf{phantom,t=0.3}{vp1,ip1,ip2,vp2} % pull proton blobs to left
\fmffreeze
% incoming proton 1
\fmfv{l=$\mathrm{p}^+$,l.a=180,l.d=8}{ip1}
\fmf{phantom}{ip1,vp1}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5, 6)}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5, 0)}
\fmfi{fermion}{vpath (__ip1,__vp1) shifted (-5,-6)}
%incoming proton 2
\fmfv{l=$\mathrm{p}^+$,l.a=180,l.d=8}{ip2}
\fmf{phantom}{ip2,vp2}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5, 6)}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5, 0)}
\fmfi{fermion}{vpath (__ip2,__vp2) shifted (-5,-6)}
}
\def\drawdebris{
% fragmented proton X_1
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),28) shifted (5, 4)}
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),16) shifted (5, 0)}
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1), 4) shifted (5,-4)}
% fragmented proton X_2
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2), -4) shifted (5, 4)}
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-16) shifted (5, 0)}
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-28) shifted (5,-4)}
% proton blobs (draw after \fmfi!)
\fmfblob{24}{vp1}
\fmfblob{24}{vp2}
}
\begin{document}
% PP COLLISION - Generic hard process
\begin{fmfpicture}{-2,44}{0,44}{pp_hard} % padding (LTRB)
\begin{fmfgraph*}(160,80) % dimensions (WH)
% external vertices
\fmfleft{ip2,ip1}
\fmfright{op2,o,op1}
\drawprotons
\drawdebris
\fmf{phantom,l.s=left,l.d=12,label=$p_1$}{ip1,vp1}
\fmf{phantom,l.s=right,l.d=12,label=$p_2$}{ip2,vp2}
% partons incoming from proton
\fmf{fermion,l.d=3,l.s=right,label=$x_1p_1$}{vp1,v}
\fmf{fermion,l.d=3,l.s=left,label=$x_2p_2$}{vp2,v}
% hard interaction
\fmf{phantom,t=1.4}{v,o} % predefine path path \fmfi
\fmffreeze
\fmfi{fermion}{vpath (__v,__o) rotatedaround(vloc(__v), 14) shifted (2, 2)}
\fmfi{fermion}{vpath (__v,__o) rotatedaround(vloc(__v), 0) shifted (2, 0)}
\fmfi{fermion}{vpath (__v,__o) rotatedaround(vloc(__v),-14) shifted (2,-2)}
\fmfblob{18}{v}
\end{fmfgraph*}
\end{fmfpicture}
% PP COLLISION - Drell-Yan
\begin{fmfpicture}{-2,44}{19,44}{pp_hard_DY} % padding (LTRB)
\begin{fmfgraph*}(160,80) % dimensions (WH)
\fmfset{arrow_len}{10} % arrow length
% external vertices
\fmfleft{ip2,ip1}
\fmfright{op2,f1,f2,op1} % add dummies 'd' for spacing
\fmfshift{8 right}{f1,f2}
\fmfshift{8 down}{f1}
\fmfshift{8 up}{f2}
\drawprotons
\drawdebris
% partons incoming from proton
\fmf{fermion,t=1.6}{vp1,v}
\fmf{fermion,t=1.6}{v,vp2}
% hard process
\fmf{boson,t=2,l.d=4,l.s=left,label=$\mathrm{Z}/\gamma^*$}{v,vf}
\fmf{fermion,t=2}{f1,vf,f2}
% labels
\fmfv{l.a=-25,l.d=3,l=$\ell^+$}{f1}
\fmfv{l.a=25,l.d=5,l=$\ell^-$}{f2}
\end{fmfgraph*}
\end{fmfpicture}
% PP COLLISION - Higgs production through gluon-fusion
\begin{fmfpicture}{-2,44}{22,44}{pp_hard_ggH} % padding (LTRB)
\begin{fmfgraph*}(160,90) % dimensions (WH)
\fmfset{curly_len}{7}
% external vertices
\fmfleft{ip2,ip1}
\fmfright{op2,o,op1}
\fmfshift{14 right}{o}
\drawprotons
\drawdebris
% partons incoming from proton
\fmf{gluon,t=1.4}{v1,vp1}
\fmf{gluon,t=1.4}{vp2,v2}
% hard process
\fmf{fermion,t=0.3}{v1,v2}
\fmf{fermion,t=1.7}{v2,vh,v1}
\fmf{dashes,t=2.8}{vh,o}
% vertices
\fmfv{decor.shape=circle,decor.filled=full,decor.size=4,f=colkappaf,
l.d=3,l.a=-65,l=\color{colkappaf}$\kappa_\mathrm{t}$}{vh}
% labels
\fmfv{l.a=0,l.d=3,l=H}{o}
\end{fmfgraph*}
\end{fmfpicture}
% PP COLLISION - Higgs production through gluon-fusion
\begin{fmfpicture}{-2,44}{36,44}{pp_hard_ggH_tautau} % padding (LTRB)
\begin{fmfgraph*}(160,90) % dimensions (WH)
\fmfset{curly_len}{7}
% external vertices
\fmfleft{ip2,ip1}
\fmfright{op2,o2,o1,op1}
\fmfshift{24 right}{o1,o2}
\fmfshift{2 up}{o1}
\fmfshift{2 down}{o2}
\drawprotons
\drawdebris
% incoming parton
\fmf{gluon,t=1.3}{v1,vp1}
\fmf{gluon,t=1.3}{vp2,v2}
% hard process
\fmf{fermion,t=0.2}{v1,v2}
\fmf{fermion,t=1.7}{v2,vh1,v1}
\fmf{dashes,t=2.5,l.s=left,label=H}{vh1,vh2}
% decay
\fmf{fermion,t=2.3}{o2,vh2,o1}
% vertices
\fmfv{decor.shape=circle,decor.filled=full,decor.size=4,f=colkappaf,
l.d=3,l.a=-65,l=\color{colkappaf}$\kappa_\mathrm{t}$}{vh1}
\fmfv{decor.shape=circle,decor.filled=full,decor.size=4,f=colkappaf,
l.d=3,l.a=-115,l=\color{colkappaf}$\kappa_\tau$\hspace{-2pt}}{vh2}
% labels
\fmfv{l.a=25,l.d=4,l=$\tau^-$}{o1}
\fmfv{l.a=-20,l.d=4,l=\vspace{-2mm}\strut$\tau^-$}{o2}
\end{fmfgraph*}
\end{fmfpicture}
% PP COLLISION - Single leptoquark production with decay
\begin{fmfpicture}{-2,44}{25,44}{pp_hard_LQ_single} % padding (LTRB)
\begin{fmfgraph*}(160,90) % dimensions (WH)
\fmfset{curly_len}{7}
% external vertices
\fmfleft{ip2,ip1}
\fmfright{op2,o3,o2,o1,op1}
\fmfforce{(1.07w,.82h)}{o1} % exact placement
\fmfforce{(1.07w,.52h)}{o2} % exact placement
\fmfforce{(0.98w,.24h)}{o3} % exact placement
% internal vertices (exact placement)
\fmfforce{(.61w,.48h)}{v1} % exact placement
\fmfforce{(.82w,.48h)}{v2} % exact placement
\fmfforce{(.94w,.67h)}{lq} % exact placement
\drawprotons
\drawdebris
% parton & photon incoming from proton
\fmf{fermion,l.d=3,l.s=right,label=b}{vp1,v1}
\fmf{gluon,l.d=4,l.s=left,label=$g$}{vp2,v1}
\fmf{fermion,l.d=5,l.s=right,label=b}{v1,v2} % s-channel
% LQ -> btau
\fmf{dashes,t=2.9,l.d=3,l.s=left,label=LQ}{v2,lq}
\fmf{fermion,t=1.7}{o2,lq,o1}
\fmf{fermion,t=0.3}{v2,o3}
% vertex
\fmfv{d.shape=circle,d.fill=full,d.si=3,f=colvtx,
l=\colvtx$\lambda$,l.d=5,l.a=66}{v1}
% labels
\fmfv{l.a=25,l.d=4,l=b}{o1}
\fmfv{l.a=20,l.d=4,l=\vspace{-2mm}$\tau^+$}{o2}
\fmfv{l.a=-20,l.d=5,l=$\tau^-$}{o3}
\end{fmfgraph*}
\end{fmfpicture}
% PP COLLISION - Single leptoquark production (photon-induced) with decay
\begin{fmfpicture}{-2,44}{16,28}{pp_hard_LQ_single_photon} % padding (LTRB)
\begin{fmfgraph*}(160,90) % dimensions (WH)
% external vertices
\fmfleft{ip2,ip1}
\fmfright{op2,o3,o2,o1,op1}
\fmfshift{6 down}{o3}
\fmfforce{(1.02w,.81h)}{o1} % exact placement
\fmfforce{(1.02w,.51h)}{o2} % exact placement
% internal vertices (exact placement)
\fmfforce{(.65w,.66h)}{v1} % exact placement
\fmfforce{(.65w,.33h)}{v2} % exact placement
\fmfforce{(.88w,.66h)}{lq} % exact placement
\drawprotons
% fragmented proton X
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),28) shifted (5, 4)}
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),16) shifted (5, 0)}
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1), 4) shifted (5,-4)}
% outgoing intact proton
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-12) shifted (9.3, 5)}
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-12) shifted (8.0,-1)}
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-12) shifted (6.7,-7)}
% blobs (draw after \fmfi!)
\fmfblob{24}{vp1}
\fmfblob{24}{vp2}
% parton & photon incoming from proton
\fmf{fermion,l.d=3,l.s=right,label=b}{vp1,v1}
\fmf{photon,l.d=3,l.s=left,label=$\gamma$}{vp2,v2}
\fmf{fermion,l.d=4,l.s=right,label=$\tau$}{v1,v2} % t-channel
% LQ -> btau
\fmf{dashes,t=2.9,l.d=3,l.s=left,label=LQ}{v1,lq}
\fmf{fermion,t=1.7}{o2,lq,o1}
\fmf{fermion,t=0.3}{v2,o3}
% vertex
\fmfv{d.shape=circle,d.fill=full,d.si=3,f=colvtx,
l=\colvtx$\lambda$,l.d=5,l.a=-45}{v1}
% labels
\fmfv{l=$\mathrm{p}^+$,l.a=-45,l.d=16}{op2}
\fmfv{l.a=25,l.d=4,l=b}{o1}
\fmfv{l.a=20,l.d=4,l=\vspace{-2mm}$\tau^+$}{o2}
\fmfv{l.a=-20,l.d=5,l=$\tau^-$}{o3}
\end{fmfgraph*}
\end{fmfpicture}
% PP COLLISION - Photon-induced ditau productions
\begin{fmfpicture}{-2,44}{16,28}{pp_hard_LQ_gg2tautau} % padding (LTRB)
\begin{fmfgraph*}(160,80) % dimensions (WH)
% external vertices
\fmfleft{ip2,ip1}
\fmfright{op2,o2,d,o1,op1}
\drawprotons
% outgoing intact proton 1
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),12) shifted (6.7, 7)}
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),12) shifted (8.0, 1)}
\fmfi{fermion}{vpath (__vp1,__op1) rotatedaround(vloc(__vp1),12) shifted (9.3,-5)}
% outgoing intact proton 2
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-12) shifted (9.3, 5)}
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-12) shifted (8.0,-1)}
\fmfi{fermion}{vpath (__vp2,__op2) rotatedaround(vloc(__vp2),-12) shifted (6.7,-7)}
% blobs (draw after \fmfi!)
\fmfblob{24}{vp1}
\fmfblob{24}{vp2}
% incoming photons from protons
\fmfforce{0.06[vloc(__vp1),vloc(__vp2)]}{q1} % exact placement
\fmfforce{0.06[vloc(__vp2),vloc(__vp1)]}{q2} % exact placement
\fmf{photon,l.d=6,l.s=right,label=$\gamma$\hspace{-4pt}}{q1,v1}
\fmf{photon,l.d=5,l.s=left,label=$\gamma$\hspace{-4pt}}{q2,v2}
\fmf{fermion,l.d=4,l.s=left,label=$\tau$}{v2,v1} % t-channel
% LQ -> btau
\fmf{fermion,t=1.15}{v1,o1}
\fmf{fermion,t=1.15}{o2,v2}
% vertex
\fmfv{d.shape=circle,d.fill=full,d.si=3,f=colvtx,
l=\colvtx\hspace{6pt}$a_\tau$,l.d=4,l.a=75}{v1}
\fmfv{d.shape=circle,d.fill=full,d.si=3,f=colvtx,
l=\colvtx\hspace{6pt}$a_\tau$,l.d=5,l.a=-70}{v2}
% labels
\fmfv{l=$\mathrm{p}^+$,l.a=50,l.d=18}{op1}
\fmfv{l=$\mathrm{p}^+$,l.a=-45,l.d=16}{op2}
\fmfv{l.a=25,l.d=4,l=$\tau^-$}{o1}
\fmfv{l.a=-20,l.d=5,l=$\tau^+$}{o2}
\end{fmfgraph*}
\end{fmfpicture}
\end{document}Click to download: pp_hard.tex • pp_hard.pdf
Open in Overleaf: pp_hard.tex